ぎょーむ日誌 2005-05-18
2005 年 05 月 18 日 (水)
-
1000 起床.
朝飯.
コーヒー.
1100 自宅発.
雨.
1115 研究室着.
-
ここ数日,
北大ネットから外部へのつながり (via http)
がよろしくない.
たぶん,
また強制通過型の proxy が腐れているのだろう
……
と思って調べてみると,
どうもそうではなさそうだ.
こちらの nameserver が不調なのか,
と思って調べてみると,
これもそうではない.
LAN 内の名前引はうまくいく.
「上流」とのつながりが悪いのか
……
と思ってるうちに回復してしまった.
やはり上流が死んでいたのか?
-
なぜかお茶部屋雑談にとらっぷされてしまう.
何やら新しいびぢねすモデル (めざせ年商 xx 億円!)
とかいうアイデアが某研究室で検討されてるみたいなんだけど,
それってすぱむ業者と同じでは,
と
……
まあ,
すぱむ屋さん,
意外ともうかりそうだけどねぇ.
-
戸外の雨はふりやむ気配なし.
昼飯にする.
-
さいきんアタマの中が
「Bayesian 的な問題解決の練習問題モード」
になってるのか
……
難しい統計モデリングになりそうなハナシを見たときに,
ほぼ無意識のうちに
「これをべいづ推定的な定式化に帰着させることができるとすれば,
どうすればよいのか」
を検討するようになってしまっている.
それはいいんだが,
必ずしも「いまやらねばならぬ問題」
ではない問題についてもそういう検討を始めてしまうので,
時間がどんどんそちらですりつぶされて,
ですね.
-
しょうがないので,
そういうときはアタマが落ちつくまで考えてから,
そこまでの結果を紙のメモ帳に書いておく.
やっぱ時間かかりますな.
-
難問を考えるのは時間のムダ,
説.
-
いったん考え出すとなかなか止まらない
-
考えるのをやめようとしてもアタマから削除できない
(暴走が制動できんかんぢ)
-
時間かかってしまったので「重要な問題だ」
と錯覚して途中経過の記録なんぞにさらに時間を費す
-
記録してるうちにまたアタマが励起されて
1. にもどる
いやはやー
-
この日,
うだうだと考えてた問題は例によって,
というか翌朝アタマがりせっとされたときになって,
マシそうな回答を思いついてしまった
……
下の図のような「左右反転」を考えればよいのだ
……!!
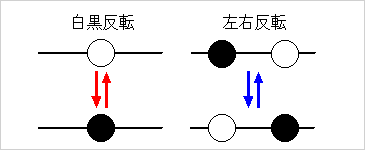
-
いきなりなんなんだ?!
と思われるかもしれないが
……
まあ,
たとえば,
生物とかの分布 (いる・いない) を「推定」するような問題
だと考えてくだされ.
生態学会の研究発表とかでよく見かけるアレで,
「ここはこういう環境だから生物 X の存在確率が高い」
というような.
つまりこれは (上の図でいう) 「白黒反転」なんかが環境に依存している,
というようなモデルと観測データの対応させかたの問題だ.
-
で,
こういうハナシを聞かされるたびに,
「こういうのって『そこに生物 X がいること』
自体も情報なんだから,
それも利用せんといかんよな」
と考えるわけで,
このあたりが近ごろ考えつづけてる
The Gibbs Distribution
だの MCMC 法だの EM アルゴリズムだの Bayesian
だのといったヨタ話と密接に関係している.
こういうモデルを考えないと集中分布とか説明できん.
-
で,
本日ひっかかっていたのは
「集中分布なら状態間の正の相互作用を考えればよい
(といった問題についてはこれまでかなりしつこく検討してきた)
……
しかし個体間に『反発力』がはたらく場合は計算がけっこう難しくなるんでは?」
というあたりだ.
これは規則分布みたいなのができてしまう状況で,
典型的には
電線の上の鳥たち
みたいな.
-
で,
反発力ある場合の
Gibbs sampling
をどうやったもんだろうかとナヤんでいたわけだが
……
上の図のように「左右反転」も加味してやればいいぢゃん
(もう少し正確にいうと,
左右反転する確率を考慮した Gibbs sampling すればいい),
と翌朝になってよーやく気づいた次第なのである.
植物みたいななかなか移動せん生きもののモデリングばかりやってると,
ついついこう「ちょっと横に動かしてみる」
といった発想が出てこなくなるんだよね
……
おそるべし.
われながらアタマがかたいな.
-
ともあれ,
この解決を考えつくのは翌朝のことで,
この日は検討もぎょーむも何の進展なくオワってしまった.
1940 研究室発.
雨.
2010 帰宅.
晩飯.
ナタデココ寒天よせ作ってみたり.
嗚呼,
何やってんだか.
-
上の「個体間反発」みたいな研究を紹介している
「なわばりの生態学」
(長谷川・種村) という本があり,
これは 1986 年出版と 20 年ちかく以前のものでありながら,
すでに Gibbs 分布だの MCMC 法
(単に「モンテカルロ法」と記述されているが)
だのパターンからの最尤推定といった問題を扱ってるぢつにスゴい本で
……
で,
生態学ではこのあたりの研究はその後 20 年間あまり進歩しておらず,
最近になってよーやく
「こういう計算方法って現象を理解するうえでとても重要だよな」
と注目されはじめた,
というような
……
いやはや,
私なんかも近ごろになって内容を理解できるようになってきた次第.
-
[今日の運動]
-
[今日の食卓]
- 朝 (1020):
米麦 0.5 合.
タマネギ・ネギ・エノキダケ・コンブ・サケの味噌汁.
- 昼 (1430):
研究室お茶部屋.
米麦 0.5 合.
タマネギ・ネギ・エノキダケ・コンブ・サケの味噌汁.
- 晩 (2100):
米麦 0.8 合.
キュウリ.
モヤシ・ニラ・ショウガ・鶏レバの炒めもの.

