ぎょーむ日誌 2001-01-20
2001 年 01 月 20 日 (土)
- 1200 起床.
- ふと思いついて,
炊飯器でパンケイキを焼いてみる.
 [炊飯器で焼いたパンケイキ]
[炊飯器で焼いたパンケイキ]
一時間以上かけたんだが
…… はっきり言ってお
いしくない.中まで火が
通ってないのである.
不精して,
いっぺんにたくさん焼こうとしたのが
敗因だな.
リリエンタール
(19 世紀のドイツのグライダー研究家)
曰く「進歩には犠牲がつきものである」.
- 夕方まで,
三次元開空度計算法の改良案を考える.
昨日,
小川データを使った計算をやっていて
「こりゃあ,
そろそろ改造したほうが良いかな」
という必要性を感じたため.
- 今のところ,
小川モデルにおいては障害物オブジェクトの
Voxel 化において 1m 立方のモノを使っているんだが
(地形は別の取り扱いになるんで 5m × 5m × 1m),
このサイズだと樹冠の葉群を表すには小さく,
一方で幹を表すには幅が広く高さが足りないのである.
- 現在の Voxel 化のやり方の限界は
以前からウスウス感じていたので,
先月中ごろに行ったライブラリー大改造においては,
将来の改良を考慮した設計になっているのである.
というか,
そのための大改造だったのである.
そのときの図をもう一度引用すると
……
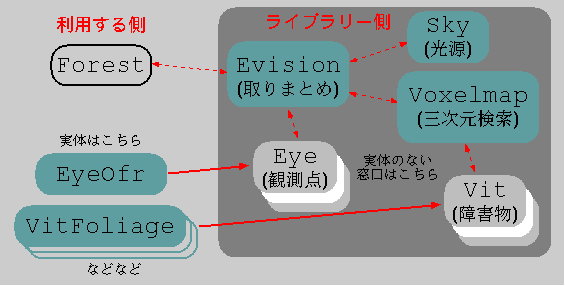
- この Vit なるものが,
いまのところは 1m 立方のソリッドな Voxel として
実現している VitFoliage なるカタチを与えられて
計算に使われている.
まあ,
なんか具体的なモノ,
というかんぢですよね.
しかしながら,
この図を最初に紹介したときに書いていたように,
Vit はもっと抽象的なオブジェクトであっても
差し支えないのである.
たとえば
「林内のとある 5m 立方 Voxel の中に存在する
三次元オブジェクトの簡単なデータベイス」
みたいな.
- つまり,
これまで PipeTree や小川モデルの開空度計算で
特徴的であった,
- 細かい Voxel を集めてオブジェクトを表現.
- それを必要最小限のメモリーに格納して
効率良く検索する
Voxelmap すなわち
map<Grid, Vit*>.
というのはヤメにして,
代わりに,
- 大きめの Voxel をとり,
その中に障害物オブジェクトの
詳細情報を格納する.
- 相対的に個数の少なくなった Voxel を
最も高速に検索できる
Voxelarray すなわち
vector<Vit*>
(まだ作ってない).
というふうに切り替えたほうが良さそうだ.
少なくとも小川モデルに関しては.
- 後者に切り替えたばあい,
最大の問題は計算時間の増大だろう.
いままで整数計算によって高速化が実現していた.
しかし Voxelarray を構成する
Voxel 数はそんなに多くないので
(おそらく現在のものに比べると 100 分の 1 未満になる),
Bresenham だのといったアルゴリズムを使っても
対して速くなるわけではない.
その代わり浮動小数点計算の量はかなり増えるはずで,
これを抑えるところがカギになりそうだ.
- どうせ今月中は
もはやのんびりとコーディングしてるヒマなさそうだけど,
上の構想がそもそも成立しうるかどうか,
いくつかのオブジェクトに関して
「視線とぶつかってるかどうか,
の当たり判定法」
に関して
計算回数を最小限にするにはどうしたらいいか,
図を描きながらあれこれと考えてみた.
- そのうちちゃんとした解説ペイジとか作るかもしれないけど,
球・
ポリゴン (三次元空間にうかぶ三角形のコト)・
円柱についての計算法はこんなふうになるか,
と思えた.
忘れんようにちょっとメモ書き.
- 球:これは視点から視線方向・障害物方向の
内積を取り (cosθを計算),
あと視点・障害物間の距離 R が分かればよい.
R sinθ
(実際には R2(1 - cos2θ))
が r (同じく r2)
より大きいか小さいか判定.
これで視線上に球がひっかかってるかわかる.
- ポリゴン:これは視点から 3 頂点へのヴェクトルを
並べた 3x3 行列 V の逆行列を計算して
視線ヴェクトルにかけたときに,
出てくるヴェクトルの要素が
全部正なら「当たり」
(のはず,要再検討).
3x3 の逆行列計算にはベタ書きした数式を使うと,
9 要素 + 3 行列式.
行列の積の計算 3 行と正負判定 3 回,
か.
家庭用ゲイム機用三次元ゲイムで
なぜ三角ポリゴン多用されるのか理由が
わかったような気がする.
三角関数とか使わない一次三元連立方程式の計算に
帰着できるからだ,
たぶん.
- 円柱:視線上に円柱あるかどうかを判定するのは
難しそうだけど,
竹中明夫さん (環境研) に教えてもらった
方法使うと比較的計算量少なくてすみそう.
私の憶測も交えつつその方法を説明すると;
円柱を (0,0,0) を起点とする
極座標ヴェクトルで表現しておいて,
その方位角・仰角ぶんだけ視点を逆回転
(自作の
Polar.Roate()
関数使うとよけーな計算増えそうだな).
円柱 (樹木の幹) 直立してるとすれば楽なんだが,
将来的には斜めに伸びるイヌブナとか
計算するかもしれんから,
マジメに回転すべきなんだろう.
これで標的の円柱が z=0 の X-Y 平面上に
の見かけに変換されるんで,
変換された視線の X-Y 平面上での交点求める.
あとはその (x,y) が円柱の X-Y 射影
(長方形の領域)
に入ってるかの大小判定 4 回.
- ……
とゆーような計算を,
視線にそって視点を 5m とか 10m ずつ動かしながら,
周囲の Voxel にらみつつやっていくわけだ.
あ,
やっぱりたいへんそう.
しかし従来方式ではやはりスケイラビリティなるものに
欠けるところがある,
と言わざるを得ないので,
そのへんに関しては今考えてるやつのほうがマシである.
- 夜になってから昼飯と称する食事を終えてから,
急に怠惰になって久しぶりに 4 時間ほど Nethack に没入.
おそるべき時間浪費ゲイムである.
今回はペットを「変化の杖」で
かなり強いモンスターに変えたところ,
ヒトの弱味につけこむ
憎むべき強欲な店主たちを次々に殺戮してくれるんで
(しかもそのことによって自分の評価は下がらない,
ペットが勝手にやったことだから),
ついつい長時間遊んでしまった.
- 真夜中近くに晩飯を食ってると,
いきなり右上小臼歯の一部が欠けてしまった.
どうやら以前から虫歯だったようである.
うーむ.
近ごろは痛まないから直ったのかと錯覚してたんだが,
実は悪化してたんだなぁ.
とほほ.
- 鏡でみると
……
ああ,
なんということか.
歯の 10% ぐらいが欠落して
「あれがエナメル質,
こちらは象牙質,セメント質
……」
と解説できるぐらいでかい断面が露出してしまっている.
けっこうショッキング.
- 冷たい水とかに触れないかぎりは痛まないんだけど,
気になるんで明日歯医者に行こう.
電話帳とネットを検索して,
日曜日でも診療してくれる歯医者を探す.
大田区内で 3 件ほどみつかったんで,
まぁ,
なんとかなるだろう.
だめなら明後日でもいいや.
- 今日の朗読
``Analytical Population Dynamics'' (Royama, 1992)
Part I Theoretical bases of population dynamics
Chapter 1 Basic properties
and structure of population processes
- 1.6 Ecological mechanism underlying population regulation
- 1.6.1 Feasibility and robustness
of population regulation
- 1.6.2 Density-dependent
and density-independent factors
- 1.6.3 Effect of ecological factors
and process structure
- 1.6.4 Fragile regulation
by a pure density-independent process
- 1.6.5 Robust regulation
by a density-dependent process
- 1.6.6 Examples of fragile and robust regulation
- 1.6.7 Negative correlation
between reproductive rate and density
in a persistent population
- 蝋山本第一章の実に三分の一 (15 ペイジ) を占拠している
第 1.6 節である.
集団の密度変化の性質を表す語として
persistence だの regulated だのと出て来て,
ここでは robust というのが登場する.
これは外部からの擾乱に対してなお persitence を
維持する性質で,
robust じゃないやつは fragile となる.
この後のながーい解説を
思いっきりはしょって
まとめると;
集団密度に無関係な density-independent な
要素だけで変化してる集団は persistence になりうるけれど,
外からノイズが入ったときにどんどんばらつくので
robust にはなりえない.
それに対して
密度にたいして再生産速度が負の相関もつような
density-dependent な機構をもつ個体群動態は robust になりうる.
ただしこれは必要条件であって
……
と感動的なまでに論理的で偏執的な著者は
第一章の残りの部分で
このあたりをツメていく予定なのである.
- このあたりで解説されてることはまさにこの本の独壇場.
古今独歩,
というやつか.
ただし本を開いていきなりこの第一章を読んでしまった
生態学者はかなりつらいキモチになるだろう.
私が先に読んだようなヤマネコ・ウサギ話などを
見ておかないと,
何でこんなことばっかりやってるのか,
ありがたみがわかりにくいのではないかと思う.
具体的な描像が頭の中にあると,
読んでいてなかなか興奮させられるんだけどね.
- しかし朗読するのは苦しい長丁場でした.
英語でたくさんの数式読みあげていくと
頭がヘンになりそう.
いんてぐらるふろむ
……
ふぁんくしょんおぶえっくすさぶてぃーぷらすわん
……
いずいくぉーるとぅ
……
- ああ,
明日は歯医者か.
- 今日の食卓
- 朝 (1320):
炊飯器で焼いたパンケイキ.
失敗作.
コーヒー.
- 昼 (1930):
米 0.5 合.
豆腐・タマネギ・ニンニクの茎のカレー.
- 晩 (2340):
米 0.5 合.
豆腐・タマネギ・ニンニクの茎のカレー.
 [炊飯器で焼いたパンケイキ]
[炊飯器で焼いたパンケイキ]
 [炊飯器で焼いたパンケイキ]
[炊飯器で焼いたパンケイキ]
