ぎょーむ日誌 2001-01-15

2001 年 01 月 15 日 (月)

• 0700 起床． 昨晩は 0100 ごろまでには寝れた．
• 朝飯・弁当の準備． 朝飯． コーヒー． 洗濯．
• 0743 自宅発． 晴れ． 燃えるゴミ出し． 今日は最低気温が氷点下ということで， 水たまりが凍結していたりする． 0759 東京モノレイル流通センター発． 浜松町の気温 -2 ℃． 急に下がったなぁ． 0820 研究所着．
• 朝一番の仕事として， めんどー感のあるメイルを一時間かけて書く． あて先は九大の矢原さんである． いや， 別に変なこと申しつけられたわけではなくて， 矢原さん的なごく真面目なご提案だったのだが． そしてマジメなことには適性のない私．
• 小川座標系を再検討． なぜか右手系で設定してしまった． ところが毎木調査と POV-Ray (三次元レンダリングソフトウェア) は左手系なんだよね …… そのうち， 全部直さんといかんようになるかも．
• なんとなく， 中村正三郎氏 のペイジに逃避してると， バイオインフォマティックスについての 話題があり …… 「生物学にとっての情報学は 物理にとっての数学みたいなものです」 …… なるほど， さうなのかもしれん．
• 先週， 錯乱状態にあった 「天球上の太陽の軌道」 問題なんだけど， 北半球の場合は たぶん下のように考えれば OK なんだろう．

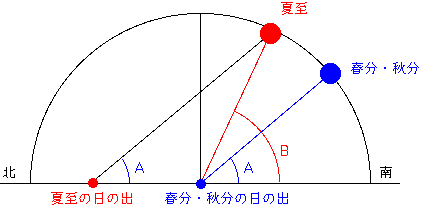
1. 春分・秋分における 太陽南中の 角度 A を求める． これは 90°- 観測地北緯．
2. 夏至における 太陽南中の 角度 B を求める． これは A + 23.5°．
3. 図のような平行線を 引っ張ると投影された 夏至太陽軌道がわかる．

あとは三角形の相似とか 三角関数とかごちゃごちゃ使うと 計算できちゃうわけだ． やはり面倒だな． 全部， 赤道上のみかけに変換するとラクになるかな． つまり， 上の図で春分・秋分点の南中高度 A が 90° になるような回転ね (反時計方向に 90°- A の回転)．
• 午前中は極座標問題考えて終わった． 昼飯の弁当食う．
• まぁ， すでに極座標クラス Polar というのを 作ってあるからそれを流用して計算してみるかな． えーと手続きとはして以下のようにやってみれば 良いのだろうか．
  1. 方眼間隔 d を決める．
  2. 極座標中心と方眼の (0, 0) を一致させる． 極座標の半径は R で固定．
  3. 方眼上の点 (x0, y0) が以下の変換のあと 最後の条件を満たすかどうか判定する． 条件を満たす点の集合を求める．
  4. 点 (x0, y0) を 半径 R の球面上に投影 (これは観測に用いた魚眼レンズの 形状に依存して決まる)． 角度θとφが出る (x1, y1, z1)．
  5. 角度θとφを y 軸回りに 反時計方向にν回転して θ' と φ' を得る (x2, y2, z2)． これは北緯ν度における観測の場合 (赤道上での 見え方に変換したのである)． Polar.Rotate( const Polar& ) 関数を使う．
  6. このときに 角度θ'とφ' の xyz 座標系の x2 がある範囲に収まってるかを 調べる． 「春分→夏至」ならば (右手座標系で) 0 <= x2 <= R * sin 23.5° である (23.5°は地軸の傾き)．
• これで正木さん (森林総研) が使ったという 「全天写真上に方眼をかけて， 春分→夏至に太陽が通過する領域の方眼点だけ 拾った」 というのを再現してるハズ．
• そうか． 上の手続き 6. では x 座標の値 x2 だけ 見ているわけだから． これだけ計算すればいいんだ． えーと「y 軸回りの回転」というのは y1 == y2 で， と …… ならば， もっと単純に x2 = x1 * cos ν - z1 * sin ν， でいいんじゃないかな． これなら， Polar クラスだとか C++ とか使わないで， Perl だけでも計算できそうだ．
• 魚眼レンズ逆変換のところ (4.) はあらかじめ 数表を作っておけば速いかな． つまり先週の山本一清さんの canopymania-ml 投稿にあったように， これは方眼上の原点となす角度 (→ θ) と原点からの距離 (→ φ) だけで計算できるんで．
• よし． Perl でやってみよう． 図学用語集 によると， 正射影が orthogonal projection で， 等距離射影は equidistant projection かな ?
• ニコンの魚眼レンズ一覧 で気になっていた「対角魚眼」というやつなんだが …… シグマ のペイジで見ると， 写真の対角線が 180°になるようなレンズ (ふつーの魚眼レンズだと四角いフィルムの中に 丸く写る)， というものだとわかった． つまりこのレンズは全天写真撮影には 使われないから考慮しなくてよい． 結局， 開空度調査に使われる魚眼レンズの投影法は 以下の三種類だけであろう．
  • 正射影 orthographic projection
  • 等距離射影 equidistant projection?
  • 等立体角射影 equisolidangle projection
• おおっと， これを書いていたら田中浩さん (森林総研) からメイルが来て，

	ニコンの型式については、8mm F8，
	すなわち等距離射影ということになります．

なるほど等距離射影だったのか． わーい， これで山本一清さんの補正式が使えるぞ．
• 原点からの距離→仰角φに変換する 数値リストを返す関数できた．
• おっと， 広島から郵便． 出張申請書を作らなければならぬ． そう， 月末に広島出張なのである．
• さてと， 方眼復元問題だが …… 座標変換と 方眼間隔を求める問題の 両方を考えなければならない． 同時に着手すると面倒になるので， まずは後者から． そうだな 「半径 1 の円内にちょうど N 個の 格子点が入るような方眼間隔を求めよ」 としてみるか．
• 2000 ごろまで苦闘して， N プラスマイナス 2 ぐらいに 収束するところまではできた． ところがあとちょっとで きちんとはまらない．
• とりあえず撤退するか． 2005 研究所発． 2025 東京モノレイル浜松町発． 野菜など買う． 2105 帰宅．
• 晩飯食ってから， ふと思いついて 「方眼を少しずらしてやると ぴったりする位置が見つかるんじゃ なかろーか」 と思いついて試してみる． つまり， モノがぴったりとはまらない場合， がたがたとゆするじゃないですか． 計算機の中でそれをやるわけです．
• システマティックにずらす方法 思いつかなかったので， 方眼間隔を変えるたびに 0〜方眼間隔の一様乱数を二つ取って 「ずらす」という操作をしてみる． ふーむ． かなり間隔がせまくなっても， 「ずらし」の効果は大きいな．
• 夜中までかかって， まあまあの結果を得る． 不思議なことに， この「ずらし」技術を使うと かならずぴったり N 個となる 方眼間隔と位置が求まるのである． どうやら， この問題の正解はひとつではなく， たくさんなのであり， 今の手法はそのひとつを見つけ出す， というものであるようだ． ま， 実用上はそれでもいい． どうせ実際に使った方眼はわからないんだから．

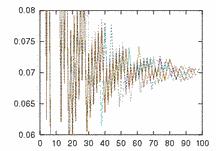[収束，かな]
だいたい 100 反復未満で
収束，ということで．横
軸は反復数で縦軸は方眼
間隔．10 回の独立試行．

• あ， もう 2400 すぎている． しょうがないんで， 今日は朗読は中止して， 明日の準備して寝ることにする．
• 今日の食卓
  • 朝 (0715): 米 0.6 合． 昨晩の味噌汁の残りで作った雑炊．
  • 昼 (1220): 弁当． 米 0.8 合． キムチ浅漬の素につけておいた ハクサイを豆腐 1/4 丁に添える．
  • 晩 (2120): 米 0.6 合． 朝と同じ．