さて,
同じデータを使って,
> library(MCMCglmm)
> fit <- MCMCglmm(cbind(y, N - y) ~ x, data = d, family = "multinomial2")
と推定してみる.
family は "binomial"
ではなく "multinomial2".
random
オプション指定の必要なし.
default ではデータの行ごとに,
R ストラクチャーなる random effects が設定されてるみたいなんだよね.
> summary(fit)
Iterations = 12991
Thinning interval = 3001
Sample size = 1000
DIC: 667.64
R-structure: ~units
post.mean l-95% CI u-95% CI eff.samp
units 6.79 3.65 10.1 480
Location effects: cbind(y, N - y) ~ x
post.mean l-95% CI u-95% CI eff.samp pMCMC
(Intercept) -4.242 -6.177 -2.523 864 <0.001
x 1.020 0.633 1.474 907 <0.001
個体差のばらつきは R-structure
(共分散ゼロの事前分布)
のところに入っていて,
これは VCV 行列の要素の事後分布を示している.
SD で表示したければ,
> summary(sqrt(fit$VCV))
Iterations = 3001:12991
Thinning interval = 10
Number of chains = 1
Sample size per chain = 1000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
2.5843 0.3304 0.0104 0.0167
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
2.01 2.35 2.56 2.78 3.34
まあ,
妥当な値.
ここでは平均値や中央値が 2.58
といった値になっているのにたいして,
glmmML()
の推定結果に示されているのは mode に近い値だろうから
(最尤推定しているので),
まあ妥当なのでしょう.
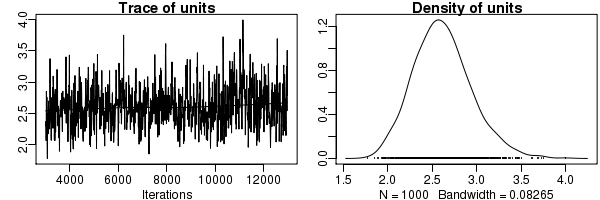
plot(sqrt(fit$VCV))