KuboLog 2007-12-30

2007 年 12 月 30 日 (日)

0950 起床．生活周期もずれてきている．なんとか修正したい．昨晩の作業のせいでコシが少しいたい．朝飯．コーヒー．洗濯．怠業してる場合ではないのに怠業．やれやれ．

1510 自宅発．曇． 1530 研究室着．さすがにヒトがいないな …… ということは，平和な年末になるのか?

昨日の Linux カーネルごたごたの片づけに 30 分ほど．

えーと，返事を書くのがイヤで二週間ばかり放置してた質問メイル．

densityで求めた経験的密度関数から直接乱数を発生させる方法って
ご存知ないですか？適当な幅決めて積分して・・ってのではなく、
rnorm的に発生させたいのです。ご存知でしたらご教示ください。

これってすごくヘンなことに使うつもりなんだろうなぁ，というニオいがぷんぷんただよってくるわけですよ …… 日ごろの彼の行動からすると．ちなみに質問者はこの研究室出身者でときどき私に上のようなヘンなメイルを送ってくる某氏．

しかしこのまま放置しとくのも今年のケガれを来年にもちこすような気分なので，歳末ススはらいの一環としてとりくんでみることに．じつはこれには「数学的には完全な回答」がある …… ただし，それって実用性なさげというか「そんな乱数発生させてなんかイミあんの?」と問うてみたい気分ではあるんだけど．

そもそもいうところの R の「density で求めた経験密度関数」とはこういうことだ．

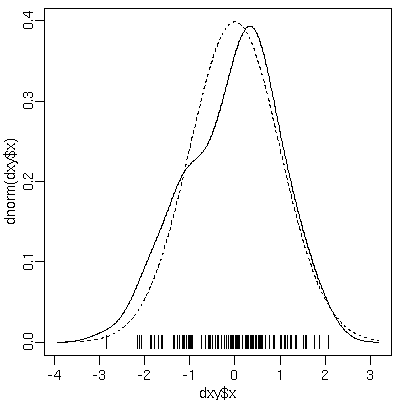
[確率密度関数の憶測]

たとえばいま平均ゼロで標準偏差 1 の正規分布 (破線) から 100 個のデータが得られたとしよう．このデータは | で示されている．この | たちが「正規分布から得られた」ということがわかっていればもともとの確率分布を推定するのはまったく簡単．しかし「どんな分布かわからん!」という状況ではどうしたらよいか? そういうときでも R の density() を使って実線で示しているような憶測確率密度関数が (推定というより) 憶測できたりする．

えーと上の憶測計算の手順としては，たとえばこういうかんぢで．

n <- 100               # データ数 n =  100 (個)
data.x <- rnorm(n)     # N(0, 1) の乱数
dxy <- density(data.x) # density() を使った推定
plot(dxy$x, dnorm(dxy$x), type = "l", lty = 2) # もとの確率分布の表示
points(data.x, rep(0, n), pch = "|") # data.x の "|" 表示
lines(dxy$x, dxy$y)       # 憶測された確率密度分布の表示

ホントは正規分布のハズなんだけど， 100 個ぐらいのデータでは上のようにぼこぼこ密度関数が憶測されてしまう．こんなアヤしげな分布から「直接乱数を発生させ」たってインチキくさいだけなんだけど，パズルとしてはおもしろい (そして MCMC 計算結果の事後分布表示に多用してしまっている density() の性質に対する理解が深まるので) ちょっと検討してみることにする．

そもそもこういうコトを検討する第一歩は help(density) (もしくは ?density) しろってコトなんだけど，そもそもこの質問者はマニュアルとかちゃんと読まないヒトで．ともあれこの R の help を読むだけで density() の挙動はいろいろわかる …… と言いたいところだけど，これはあるていどはカーネル密度推定なるものを勉強したことがあるヒトでないと「このバンド幅って何?」となるかもしれない．

より詳しい解説は例によって例のごとく MASS4 本 5.6 節 Density Estimation に書かれていたりする．

このぎょーむ日誌にまた数式画像ファイルとかはりつけて解説すんのは面倒なので (おお，ゐきぺでぃあにはちゃんとした数式とわかりやすい図が示されているなぁ)，「上のような憶測ぼこぼこ密度関数がどのように生成されているのか?」を R コードで示すことで説明にかえたい．ここで自作のカーネル関数 K() とカーネル密度推定値の vector fx を (上の作図 R コードのつづきで)

K <- function(xj) dnorm(dxy$x, xj, dxy$bw) # xj は data.x のある値，ですな
fx <- apply(sapply(data.x, K), 1, mean) # それを全ての data.x の値について「ならす」

と定義してみる (default では density() のカーネル関数は正規分布なので dnorm() を使っている)．さっきの図のつづきで，このカーネル密度推定値の曲線を赤でを上書きしてみよう．

lines(dxy$x, fx, col = "#ff4000")

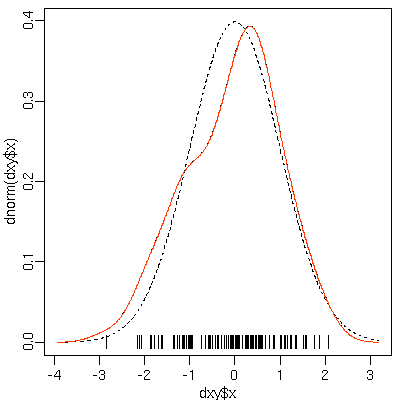
[density() 計算の再現]

もとの density() 推定値の上にぴったり重なっていますよー，とゆー図．つまり density() の内部でやってることを K() 関数と fx 計算で完ペキに再現できてますよー，ゆーコト．

さてさて， density() のしくみはかなり簡単だと確認できたので，ここから乱数を発生させるような関数を定義するのは簡単にできる．たとえば rdensity() と名づけた関数の実装例は ……

rdensity <- function(n, x)
{
	dxy <- density(x)
	K <- function(xj) dnorm(dxy$x, xj, dxy$bw)
	rnorm(n, mean = sample(x, n, replace = TRUE), sd = dxy$bw)
}

ようするに，データから density() 計算して，カーネル関数定義して，

データ内の一個をランダムに選ぶ (sample())
そこを中心にして SD = バンド幅となる正規乱数を発生させる

という簡単なことだ．これはくだらないと思われるかもしれないけれど， density() が生成する確率密度関数の定義と完全に首尾一貫している乱数発生方法になっている．で，くだらないついでにかくのごとく発生させた乱数とさらにそこからもういちど憶測させた確率密度を図示してみる．

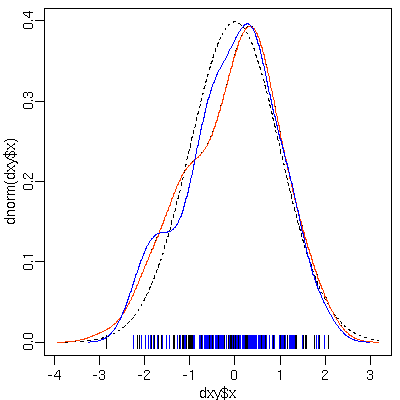
[rdensity() 乱数]

青の | が rdensity() から得られた 100 個のサンプル．さらに青線はその標本から再憶測させた density()．ウソにウソを重ねているというか，どんどん「真の分布」から乖離していくような ……

いやー，やってみたけどやっぱ density() からのサンプリングって意味不明でインチキくさいよ …… えーい，何やら邪悪な目的のために使うんだろうなぁ，と懸念しつつ返信メイルかき． rdensity() の関数定義だけのせる．説明は「明日公開のぎょーむ日誌みろ」ですませておくか．

...
さて，ご質問の件ですが，
これは「density() が何をどうやっているか」がわかれば簡単にわかる問題で
す．答えだけ示すと

rdensity <- function(n, x)
{
	dxy <- density(x)
	K <- function(xj) dnorm(dxy$x, xj, dxy$bw)
	rnorm(n, mean = sample(x, n, replace = TRUE), sd = dxy$bw)
}

これで rdensity(100, データの vector) などとすると御所望の乱数が 100 個
ばかり得られます．もうちょいくわしい説明は明日公開のぎょーむ日誌でも見
てください．この関数は density() の挙動に完全にあわせたモノになっている
のできわめて「正確な」乱数発生関数になっています …… ただし，私として
は density() なんぞで憶測されたアヤしげな確率密度関数を使って何かさらに
計算するってのがひどく危険なことのように思えます．とても邪悪な目的に使
われそうな気がしますね……

> コネタですが、某国立環境研PD氏にwinBUGSを布教しました。
> 今trap窓と激しい戦いを繰り広げているようです。
> 徐々に広がるべいぢあん・・・

貴君とヤツほど「ゐんばぐす Trap 窓地獄のどん底で子豚のごとくきーきーと
暴れまわる」ことが似つかわしい若手研究者もなかなかいないよなぁと思わず
にはいられません．

よいお年を．

さてススはらいは一件すんだ．もひとつは昨日だかに書いた「著者に何をいってもムダなので断りたい査読報告かき」だが ……

1/8 提出の生態学会大会ポスター発表の要旨をひねくってみる．

2145 研究室発．さすがに寒い．買いもの． 2205 帰宅．晩飯の準備．晩飯．

[今日の運動]

すごく不健康な年末 ……

[今日の食卓]

朝 (1020): 米麦 0.8 合．ヒジキごはん．ダイコン・ニンジン・ジャガイモの味噌汁．
昼 (1340): 米麦 0.6 合．ダイコン・ニンジン・ジャガイモの味噌汁．ゆでホウレンソウ．ダイコンの酢のもの．プチトマト．
晩 (2240): 米麦 0.8 合．ダイコン・ニンジン・ジャガイモの味噌汁．コマイ．

ぎょーむ日誌 2007-12-30

2007 年 12 月 30 日 (日)