ぎょーむ日誌 2007-06-12
2007 年 06 月 12 日 (火)
-
0830 起床.
コーヒー.
朝飯.
1000 自宅発.
晴.
1015 研究室着.
-
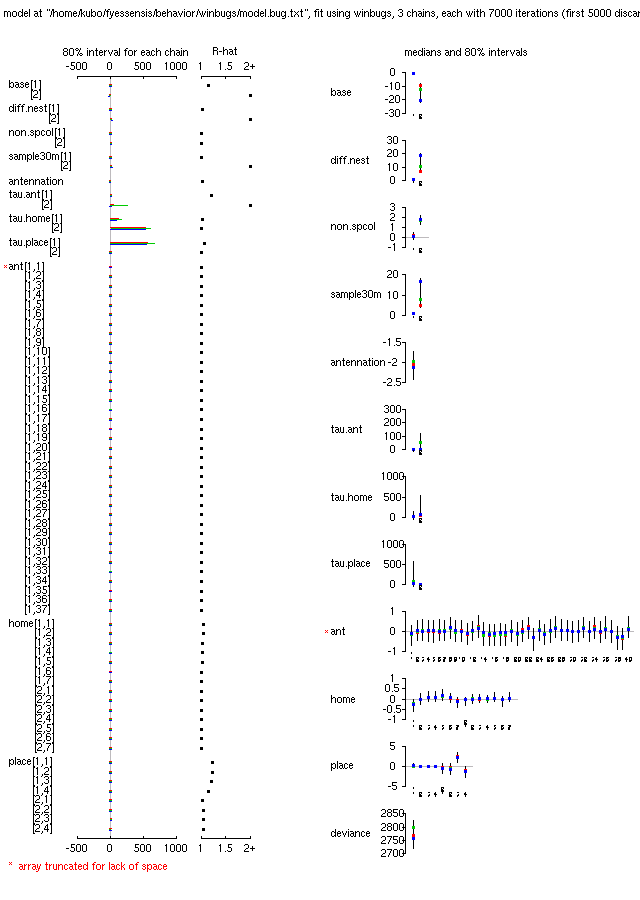
昨日の計算結果でた
……
収束もうちょい.
まだモデルの改良が必要だ.
-
こうなる原因はおそらく定山渓アリの異様な凶暴さ (攻撃頻度がすごく高い),
と何か関係ありそう.
-
定山渓アリが home で勝負する実験は 1 set しかない
-
しかもそれは巣から 30 m 離れた「同巣」
(とされてる)
定山渓アリに対するものしかない
つまり「定山渓 home」 & 「定山渓 vs 定山渓バトル」
& 「30 m 離れたところから sampling」
が交絡している特殊な状況で,
「攻撃」が異様な頻度で発生している,
とういことで攻撃まわりのパラメーターが収束してくれません,
と.
-
攻撃に関するモデルをもうちょい簡素化して再計算を命じる.
2000 MCMC step ぐらいで収束してくれないかしらん
……
よし,
収束は格段に改善された.
-
なぜか「アリの『個体差』の分散」パラメーターの収束だけが悪い.
個体差が多いので収束に時間かかる,
ということかしらん?
とりあえず初期値の与えかたで何とかならんかと試行錯誤してみる.
なぜか antennation 受けやすさの
「個体差」
がときどき小さくなりすぎるんだよね
……
-
メイル書いたり要旨とか書いたりしながらモデルの改良.
アリ「個体差」は一種類でよさそう,
とわかってきた.
というのも触角によるしつこいチェック (antennation)
受けたアリは攻撃されることはまれであるからだ
……
攻撃される場合は「こいつは敵だ!」と瞬間的に
判断されて攻撃される確率がかなり高い.
-
といろいろ工夫して 2000 MCMC step (計算時間約 600 秒)
でだいたい収束するようになった
……
と思ったけど,
詳細にみてみるともうちょっとだけ計算時間をのばしたほうがよさそう,
ということで 3000 MCMC step にしてみる.
-
アリ研究会の要旨を
でっちあげて
提出してしまう
……
こういうでっちあげは自分のクビをしめるようなもんだけど,
まあ緊急避難的に.
少なくとも行動解析の階層ベイズモデルについては
エラそーな発表ができるだろう.
-
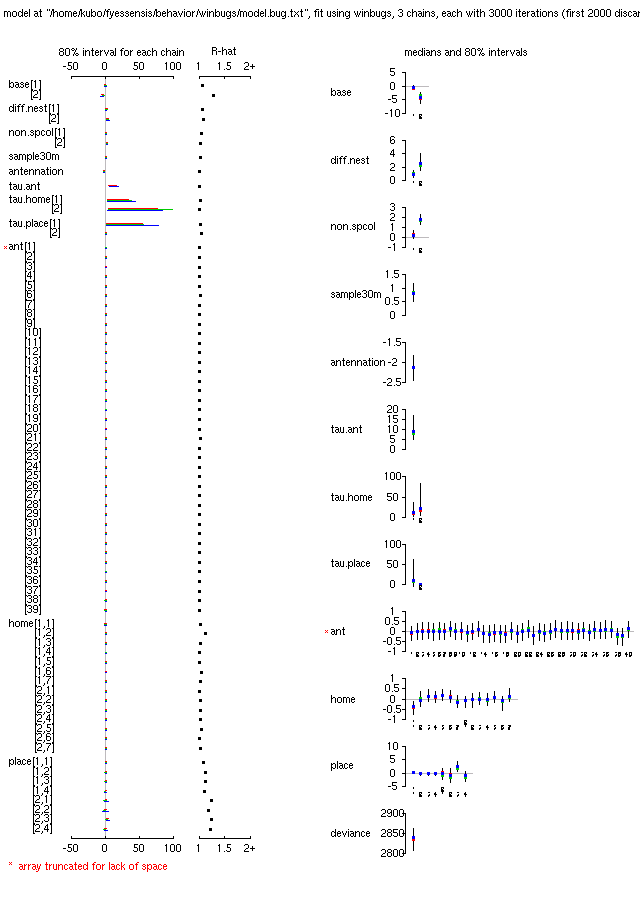
拉致られアリ計算,
330 個体のアリ「個体差」の幅をさらに制約すると,
計算がうまく収束するようになった.
-
これで収束するとなると,
少し欲がでてしまってもうちょいモデルを複雑化したくなるね.
make save
しておいてから,
攻撃モデルに「30 m 遠方効果」いれてみる.
はてさて,
どうなることやら
……
と計算させておいて昼飯.
-
今日は札幌のほうが那覇より気温たかかったそーで
……
明日も暑いみたいだ.
この季節,
北海道は寒暖の差が極端だねえ.
-
……
やはり複雑化モデルはダメ,
とわかった.
まあ現状のままで十分に現象は説明できてるような.
-
「(実験対象である) 拉致られアリがだんだん『疲れて』くる」
効果はどうだろう?
といれてみてまた試しの計算.
その間,
トドマツメイル書き.
-
1000 秒ちょいで計算終了.
ふーむ,
antennation に関しては「疲れ」
(
trial)
効果はないけど,
攻撃を受けることに関してはやっぱりはっきりした傾向あるみたいね.
「アリのココロの中」
モデリングする隠れ状態「負け犬」効果は今回は導入できそうにないけど,
「個体差」 + 「疲れ」で説明できたことにしようかな
……
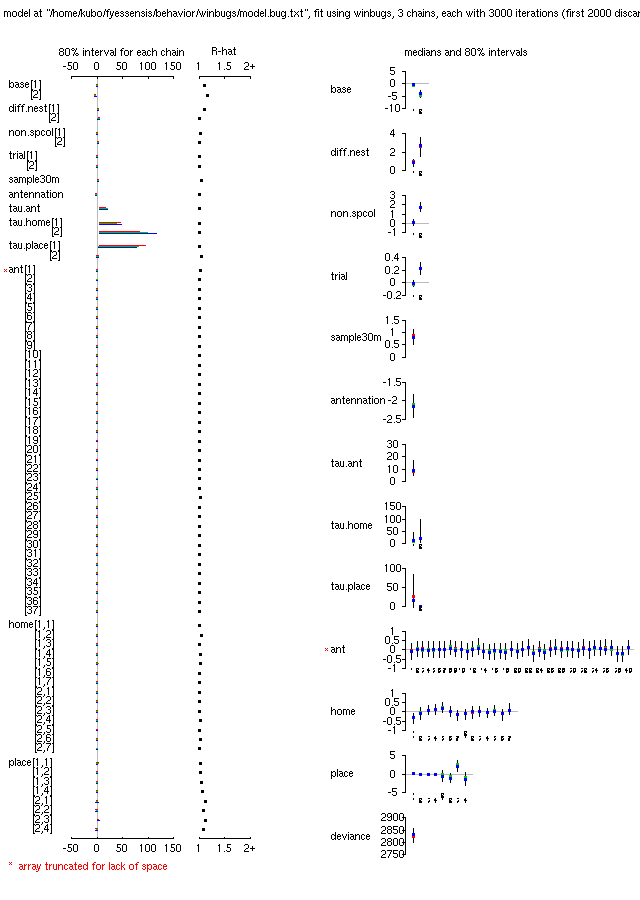
plot(ant.bugs)
は下の図のとーりで,
Table 形式の
print(ant.bugs, digits.summary = 2)
はこちらに.
-
ふーむ,
antennation または攻撃の確率のオッズ (リスク) がいろいろな要因の
係数 (パラメーター) で変わるわけだが,
これらパラメーターの事後分布 (の,そーですね,今回は平均値)
みていくと,
いろいろと興味ぶかい
……
-
同巣の場合にくらべて,
相手が巣が異なる個体だと,
antennation されるリスクは 2.4 倍,
攻撃されるリスクは 14 倍上昇
-
これが石狩浜スーパーコロニー外から来たとすると,
上の値にさらに
antennation されるリスクは 1.2 倍,
攻撃されるリスクは 5.8 倍上昇
-
拉致られアリの接触回数 (1-5 回)
が増えるにつれ,
攻撃されるリスクは 1 回ごとに 1.2 倍ずつ増える
(5 回目だと 3 倍!)
……
これが上でいう「疲れ」効果
-
巣から 30 m 離れたところから拉致されてきたアリが
攻撃されるリスクは 2.3 倍上昇
-
逆に,
いったん antennation されると
攻撃されるリスクは 0.1 倍に
……
antennation されてる間に逃げ出すスキがあるから?
-
このデータでは
「特別にアヤしまれる・攻撃されるアリあるいは出身巣」
は見つけられなさそう
……
つまり異なる巣出身かどうか,
スーパーコロニー外から来たかどうか,
が判断の上で重要
-
antennation に関しては「実験場所」の効果はとくにないけど,
攻撃しやすさに関しては
星置の巣のワーカーを 1 とすると,
オッズ比が厚田 = 1.7, 忍路 = 0.8, 定山渓 = 27
となっていて定山渓のいよーな攻撃性が
……
と言いたいところで平均値 (中央値もだいたい同じ)
はこうなってるんだけど,
じつはこの「実験場所」効果の事後分布はどれも
95% 信頼区間内にゼロを含んでいる
(おそらく厚田・忍路・定山渓は観察回数が格段に少ないため)
ので,
そういうパラメーターであるという保留つき
-
いきなり「計算おわった」脱力感が.
いや,
このアリの行動実験解析にしても事後分布図を作ったり,
説明を書いたりとかいろいろあるんだけど
……
とりあえず A801 院生部屋 Dell 機はまたしばらく休眠させようか.
自分の机の上から
sudo shutdown -h now
発令してから,
主電源のスイッチを切りにいく.
-
気分転換のため,
八甲田「脱」割算値メイルかき.
これまたいろいろと考えてしまって,
なかなか時間がかかる.
-
いろいろ論文ダウンロード,
とか.
-
データ解析こんさるメイル書き.
一般化線形混合モデル計算関数
glmmML()
(あるいは R の
help)
でいろいろ出てくる「えらー」について.
こういう例で説明してみましょうか……
> library(glmmML)
> y <- rpois(100, exp(1 + rnorm(100, 0, 1)))
> id <- 1:100
> glmmML(y ~ 1, cluster = id, family = poisson)
Call: glmmML(formula = y ~ 1, family = poisson, cluster = id)
coef se(coef) z Pr(>|z|)
(Intercept) 1.07 0.116 9.18 0
Standard deviation in mixing distribution: 0.917
Std. Error: 0.0923
Residual deviance: 241 on 98 degrees of freedom AIC: 245
これは「切片」だけモデルで,fixed effects の部分が 1 (正しく推定されてます
ね),そして linear predictor にくっつく平均 = ゼロ かつ SD = 1 の正規分布が
random effects をあらわしています.この SD の推定値はご指摘のとおり Standard
deviation in mixing distribution: に 0.917 と (だいたい正しく) 推定されて示
されていますね.蛇足ながらその下の Std. Error: 0.0923 は上の 0.917 なる推定
値の推定のばらつきです.
上の例で,私のところで生成した乱数例で計算してみると,mean(y) = 4.4 の
var(y) = 24.8 となりポアソン分布からの overdispersion になっており,これを説
明するためには random effects が必要です.上の例では linear predictor にくっ
つく平均ゼロの正規分布を使ってそれをモデル化していて,この正規分布の SD を上
のように推定してます.
さてさて,この random effects が大きかろうがゼロに近かろうが,切片の推定値に
「自信のなさ」はつきまとうものであり,これはデータ数の大小その他あれこれでき
まります.これが推定値の se(coef) となります.
1945 研究室発.
2000 帰宅.
晩飯.
[今日の運動]
[今日の食卓]
- 朝 (0930):
米麦 0.7 合.
ネギ・豆腐の味噌汁.
キャベツ・ニンジン・キュウリのサラダ.
- 昼 (1400):
研究室お茶部屋.
イソップベイカリーのバゲット.
リンゴ.
- 晩 (2100):
マカロニ.
ピーマン・トマト・バジル・豆腐のソース.
キャベツ・ニンジン・キュウリのサラダ.
イソップベイカリーのバゲット.



