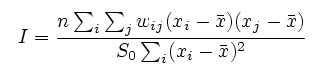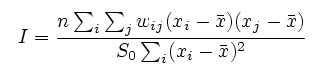「ぎょーむ日誌」目次に戻る | KuboWeb top に戻る | twilog | atom

ぎょーむ日誌 2005-03-21

苦情・お叱りは，たいへんお手数かけて恐縮ですが，久保 (kubo@ees.hokudai.ac.jp) までお知らせください．

本日 (kubolog20050321) | 次の日 | 1 日前 | 7 日前 | 31 日前 | 365 日前 | top

2005 年 03 月 21 日 (月)

0740 起床．朝飯．コーヒー． 1000 自宅発．晴． 1015 研究室着．
どーみても相関あるようには見えん，苫小牧 leafminer 季節変化，しかしながら村上さんはしぶとく何か相関あるはず，と信じているよーで．顧客がそう信じているのであればモデル商売やってるものとしては，計算せざるをえない．計算すればけりがつく．
で，また独自にいろいろと工夫してもいいんだけど，本日は趣向をかえて R の空間統計学 package のひとつ spdep を使ってみることに．いままで使ったことないんで，いろいろと調査が必要になる (…… ので「自分で作る」という方向にハシりがちなのである，とか言ってみる)．
まず距離加重行列 m を作る．これは「となり」からは影響あるけど，それより遠くからは影響ない，という加重になってる．

	> m <- matrix(0, 10, 10)
	> for (i in 1:9) { m[i, i + 1] <- 1; m[i + 1, i] <- 1}
	> m
	      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
	 [1,]    0    1    0    0    0    0    0    0    0     0
	 [2,]    1    0    1    0    0    0    0    0    0     0
	 [3,]    0    1    0    1    0    0    0    0    0     0
	 [4,]    0    0    1    0    1    0    0    0    0     0
	 [5,]    0    0    0    1    0    1    0    0    0     0
	 [6,]    0    0    0    0    1    0    1    0    0     0
	 [7,]    0    0    0    0    0    1    0    1    0     0
	 [8,]    0    0    0    0    0    0    1    0    1     0
	 [9,]    0    0    0    0    0    0    0    1    0     1
	[10,]    0    0    0    0    0    0    0    0    1     0

で，この square spatial weights matrix を weights list object (listw) おぶぢぇくとなるものに変換する．

	> lw <- mat2listw(m)
	> lw
	Characteristics of weights list object:
	Neighbour list object:
	Number of regions: 10 
	Number of nonzero links: 18 
	Percentage nonzero weights: 18 
	Average number of links: 1.8 
	Weights style: M 
	Weights constants summary:
	   n  nn S0 S1  S2
	M 10 100 18 36 136

たとえば「となり」どうしがたいへん似ているデータで Moran の I 統計量なんぞを計算させることができる．

	> moran(1:10, lw, 10, Szero(lw))
	$I
	[1] 0.77778
	$K
	[1] 1.7758

で，ならべかえ検定とかでこれの p 値なるものを計算させると (試行回数 999 回) ……

	> moran.mc(1:10, lw, 999)
		Monte-Carlo simulation of Moran's I
	data:  1:10 
	weights: lw  
	number of simulations + 1: 1000 
	statistic = 0.7778, observed rank = 999, p-value = 0.001
	alternative hypothesis: greater

まあ， p-value とかいうのが 1000 ぶんの 1 である， 999 回ならべかえたどのパターンより 1:10 なるならびかたから導出される I = 0.7778 ってのが「逸脱した」値でありました，ってこと．これはあたりまえのハナシで，可能なならべかえ総数は 10! = factorial(10) = 3628800 とーりあるわけだけど，その中で 1, 2, 3, ..., 10 と同じぐらい「となりどうしが似ている」パターンは 10, 9, 8, ..., 1 ぐらいのもんだからねえ．
…… という説明は正しくない，ということがわかった．なぜかというと I 統計量は順序統計量ではないからだ．上で定義したような距離加重行列 m を使ったときに 1, 2, 3, ..., 10 より Moran の I 統計量が大きくなる例として，以下のようなものがある，とわかってしまった．
```
	# obsI = 0.777778, pattern:  [1]  1  2  3  4  5  6  7  8  9 10
	# I = 0.818182, pattern:  [1]  4  1  2  3  6  7 10  9  8  5
	# I = 0.811448, pattern:  [1]  8  9 10  7  5  1  2  3  4  6
	# I = 0.818182, pattern:  [1]  8 10  9  7  6  4  1  3  2  5
	# I = 0.811448, pattern:  [1]  7  9 10  8  6  4  2  3  1  5
	# I = 0.784512, pattern:  [1]  6  5  2  3  1  4  7  9 10  8
	# I = 0.777778, pattern:  [1]  7 10  8  9  5  3  1  2  4  6
	# I = 0.811448, pattern:  [1]  7  8  9 10  6  2  1  3  4  5
```
うーむ …… たしかに近傍どうしは似てるけど，これってそんなに「良い」パターンなのかしらん?
まあ， I 統計量の定義から言って，注目しているふたつの量 x_i と x_j が全体の平均値から同じ方向にずれてる，というのが重要なわけで．

とすると上の「良い」パターンたちはことごとく，平均値 5.5 をはさんでいる 5 もしくは 6 が「はしっこ」のほうにいるよね．そういう状況では I 統計量の値が高くなるわけだ．
えーい，しかしながら 5 もしくは 6 が両端でなくても I が大きい場合も探せば見つかるぞ．
```
	# I = 0.79798, pattern:  [1]  4  2  1  3  5  7  6  8  9 10
	# I = 0.81818, pattern:  [1]  4  3  1  2  5  8 10  9  6  7
```
そうですなぁ …… これの場合は平均値 5.5 をはさむ「となりどうし」は一ヶ所ってのは 1, 2, ..., 5, 6, ..., 10 というならびかたと同じだけど，なぜかしら I はさらに高くなってしまう，と．
あ，わかった．両端 (となり数が少ない) に 1 とか 10 みたいな平均値からのずれてる値が来ると，ソンになるんじゃないかしらん? 上の定義で二重和とるところに注目せよ --- ほら，こういうふうに．

	> moran(c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10), lw, 10, Szero(lw))$I
	[1] 0.77778
	> moran(c(2, 1, 3, 4, 5, 6, 7, 8, 10, 9), lw, 10, Szero(lw))$I
	[1] 0.84512
	> moran(c(3, 1, 2, 4, 5, 6, 7, 9, 10, 8), lw, 10, Szero(lw))$I
	[1] 0.88552
	> moran(c(4, 1, 2, 3, 5, 6, 8, 9, 10, 7), lw, 10, Szero(lw))$I
	[1] 0.87205

こういうのもイヤなんで，何か対策をたてたい．原因の一端は上でみるように「はしっこ問題」にある．ならば，「はしっこ」が「不利」にならないように距離加重行列を変更するとどうか?

	> m
	      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
	 [1,]    0    2    0    0    0    0    0    0    0     0
	 [2,]    1    0    1    0    0    0    0    0    0     0
	 [3,]    0    1    0    1    0    0    0    0    0     0
	 [4,]    0    0    1    0    1    0    0    0    0     0
	 [5,]    0    0    0    1    0    1    0    0    0     0
	 [6,]    0    0    0    0    1    0    1    0    0     0
	 [7,]    0    0    0    0    0    1    0    1    0     0
	 [8,]    0    0    0    0    0    0    1    0    1     0
	 [9,]    0    0    0    0    0    0    0    1    0     1
	[10,]    0    0    0    0    0    0    0    0    2     0

このよーに改善してやれば …… ほーら， 9999 回のならべかえやっても，

	> moran.mc(1:10, lw, 9999)
		Monte-Carlo simulation of Moran's I
	data:  1:10 
	weights: lw  
	number of simulations + 1: 10000 
	statistic = 0.8909, observed rank = 10000, p-value = 1e-04
	alternative hypothesis: greater

ちゃんと observed rank = 10000 つまり 1:10 の「逸脱」ぶりが示されるわけで．

しかし回数を 10 万回とかにしてみたりすると …… I 統計量がさらに「逸脱」する例とかいくつか見つけやがる ……
```
	# I = 0.90303, pattern:  [1]  4  2  1  3  5  6  7  9 10  8
	# I = 0.89091, pattern:  [1]  4  3  1  2  5  6  7  8 10  9
	# I = 0.92121, pattern:  [1]  1  2  3  4  5  6  7  8 10  9
```
やれやれ．まー，事象発生確率が 10000 ぶんの 1 未満とか阿呆らしい世界をこれ以上調べなくてもいいや．
ともかく，ここでわかった重要なことは，距離加重行列を行ごとに規格化 (とゆーか edge effect の補正) したほうがよろしい，ということで．そのように改善しても，両端問題は完全に解決するわけではないんだが，
```
	> moran(c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10), lw, 10, Szero(lw))$I
	[1] 0.89091
	> moran(c(2, 1, 3, 4, 5, 6, 7, 8, 10, 9), lw, 10, Szero(lw))$I
	[1] 0.95152
	> moran(c(3, 1, 2, 4, 5, 6, 7, 9, 10, 8), lw, 10, Szero(lw))$I
	[1] 0.93333
	> moran(c(4, 1, 2, 3, 5, 6, 8, 9, 10, 7), lw, 10, Szero(lw))$I
	[1] 0.86667
```
見ればわかるように，さっきよりは多少はマシでしょう．ランダムなならべかえにおいても，「より逸脱」パターンの発生頻度が 100 倍程度は小さくなったわけで．
というような library(spdep) 調査をいったん中断して昼飯．
さて，ここまで調べてきた spdep の randomization test moran.mc() がそのまま使えるかどうか，だが …… なんかダメっぽいような気がする (plot ごとに樹木のいれかえが必要だろう)．計算関数である moran() は使えるけどね．
1 season の中に 5 plot あって，という面倒なるデータ構造は距離加重行列のカタチにも影響する．うだうだとそのような行列を生成する関数をこしらえる． season1 → season2 全樹種 268 × 268 の距離加重行列を図示すると下のようになった．この変てこなる行列は村上行列とよぶことにしよう．

樹種のあつかい，どうしたもんか，と一瞬なやむけど，とりあえず安直な手口で片づけることに．
で，いろいろと試行錯誤をつみかさねて，樹木いれかえ randomization による Moran I 統計量の確率分布の評価，というのができた．ざっとみると，やはりほぼ無相関なよーで．

	> load("timechange.RData")
	> summary(as.factor(df.timechange$Sp[is.na(df.timechange$r12) == FALSE]))
	 Am  Ap Cac  Mk  Mo  Qc  Tj 
	 56  20  11   6  10 138  27 
	> source("timechange.R")
	> moran.test.mc(2000, df.timechange) # 全樹種
	r12 : n = 268, Observed I = 2.98e-02, p = 0.064
	r23 : n = 280, Observed I = 2.93e-02, p = 0.783
	r34 : n = 325, Observed I = 8.05e-02, p = 0.584
	> moran.test.mc(2000, df.timechange[df.timechange$Sp == "Qc",]) # ミズナラ
	r12 : n = 138, Observed I = 1.12e-02, p = 0.697
	r23 : n = 139, Observed I = 2.20e-01, p = 0.004
	r34 : n = 139, Observed I = 1.38e-01, p = 0.724
	> moran.test.mc(2000, df.timechange[df.timechange$Sp == "Am",]) # イタヤカエデ
	r12 : n = 53, Observed I = 7.99e-02, p = 0.396
	r23 : n = 59, Observed I = 9.14e-03, p = 0.827
	r34 : n = 37, Observed I = -2.08e-02, p = 0.882

関連する図: leafminer 時間変化の最近傍との関係と地図．計算法のあれこれ:
- 距離加重値については平尾君のほうの logistic model と同じ関数を使う
- 14m 離れた樹木の影響まで入る
- 14m 以内に樹木がいない個体は I 統計量計算から除く
- I 統計量は全 plot で評価する --- 異なる plot の樹木との間の加重はゼロ
- randomization の回数は 2000 回
このあたりの報告メイルおくる．時刻はすでに 1920 か．
1940 研究室発． 2020 帰宅．晩飯．
夜中にごそごそと大阪大会の次の新潟大会がらみの雑用なんぞを．
[今日の運動]
- 腹筋運動 30 × 3 回．腕立ふせ 5 × 3 回．
[今日の食卓]
- 朝 (0840): 米麦 0.7 合．モヤシ・油揚・コンブの味噌汁．
- 昼 (1410): 研究室お茶部屋．米麦 0.7 合．モヤシ・油揚・コンブの味噌汁．
- 晩 (2210): 米麦 0.7 合．煮豆たきこみ飯．コマツナあえもの．

本日 (kubolog20050321) | 次の日 | 1 日前 | 7 日前 | 31 日前 | 365 日前 | top

KuboLog | KuboWeb