Experiments in ecology
Their logical design and interpretation using analysis of variace
A. J. Underwood, Cambridge University Press
輪読会メモ 1999.01.20 担当:久保拓弥 (kubo@ees.hokudai.ac.jp)
![[*]](foot_motif.png)
- さて要因実験で,もし交互作用が有意になったら,
どうするか?
7.7 節で一因子実験で述べたのとまったく同じように
解析すればよいのである.
演繹的な仮説( a priori)
![[*]](foot_motif.png) 一方で,
帰納的な仮説( a posterior)
一方で,
帰納的な仮説( a posterior)
![[*]](foot_motif.png) について調べている場合は,
以前に議論した
Type-I エラーに関する注意を思い出し,
Student-Newman-Keuls (SNK) 検定 あるいは
Ryan の検定
を行えばよい.
について調べている場合は,
以前に議論した
Type-I エラーに関する注意を思い出し,
Student-Newman-Keuls (SNK) 検定 あるいは
Ryan の検定
を行えばよい.
- つまりやることは,
- まず,ある因子のひとつの水準(level) を決める(固定する).
- 次にその水準において別の因子のすべての水準間の
多重比較を行う.
- すべての因子,すべての水準において上の二つを行う.
Table10.9 ではカサガイの例を用いてそのやり方を具体的に
説明している.
この結果は,
カサガイの死亡率が
「カサガイの密度(こみあい)」と「ソウ類の被度」
それぞれによってだけで決まっているだけでなく,
「ソウ類の被度が高くなると,密度効果がますます高くなる」
ことが多重比較から説明できる.
- 交互作用に有意差がなければ,
それぞれ有意な主効果(main effect) ごとに
多重比較をやればよい.
交互作用がないんだから,
調べている因子以外の因子に関しては,
平均をとってしまっていいのである.
- Table10.10 の例は10.9 によく似ているけど,
今度は交互作用が有意でなかった場合である.
二つの因子は独立なので,
Table に示しているとおり
それぞれの標準誤差が計算できる.
- このTable に示されている結果では,
「カサガイの密度」と「ソウ類の被度」が
それぞれ独立に死亡率に影響を与えている.
- すでに8.6.2 節で述べたように,
こういった多重比較はType-I エラーの危険を増やさないように
注意深く行わなければならない.
たとえばTable10.9c では5個のSNK 検定を
べつべつにやっているのである.
- 検定の数に会わせて有意水準を変れば確率を補正できる.
あるいはことによったら,
Bornferroni 補正を使うのがいいのかもしれない.
Table10.9 のように5回検定をやるときには
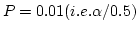 とすればよい.
とすればよい.
- こうやってType-I エラーについて操作しているときに,
もっと重要なのは検出力が
なくなってしまわないように注意することだ.
Miller(1981) は,
このように一連の検定をひとつの`familiy' であるかのように
とりあつかったために
エラーの率を操作することに起因する問題について議論している.
だけどType-I エラー問題を考慮しつつ
Type-II エラーが大きくなり過ぎないようにする方法については
簡単なやり方がない.
- もし交互作用が有意でなく,
しかもプールできないなら,
こういった解析は面倒なことになる.
Table10.12 に示した例を考えよう.
因子A が処理であり,
ふつーこちらのほうが自由度が低い.
だから検出力が高いとは言えず,
水準間でよっぽど差がないとなかなか効果が検出されない.
じつはまだ問題があって,
A に対するA
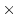 B の交互作用という
B の交互作用という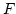 -検定は,
ホントの
-検定は,
ホントの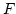 -比の近似値しか計算できていない,
ということである.
-比の近似値しか計算できていない,
ということである.
- この「A
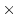 B に対する因子A の検定」は中心化された
F分布を用いるためには,
因子A の異なる水準間のデーターの分散・共分散行列に
ある対称性の性質が成立していないといけない.
このためには……
B に対する因子A の検定」は中心化された
F分布を用いるためには,
因子A の異なる水準間のデーターの分散・共分散行列に
ある対称性の性質が成立していないといけない.
このためには……
- この交互作用の検定でほとんどのことはできる.
もし
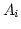 の
の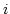 が変わったときに,
が変わったときに,
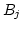 や
や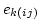 との相関が変わっているなら,
交互作用があるといってよいだろう.
交互作用があれば,
因子A とB の主効果については検定しなくてもよい.
交互作用がなければ,
因子ごとにプールしてふつうにF 検定をやればよい.
問題なのは交互作用がなくてプールできないときだ.
との相関が変わっているなら,
交互作用があるといってよいだろう.
交互作用があれば,
因子A とB の主効果については検定しなくてもよい.
交互作用がなければ,
因子ごとにプールしてふつうにF 検定をやればよい.
問題なのは交互作用がなくてプールできないときだ.
- あと「つりあいのとれた
![[*]](foot_motif.png) データー」に関して
比較的ささいな問題がある.
この場合は交互作用を検定できる簡単な方法はない.
だからデーターは「つりあいがとれる」ようにとるしかない.
データー」に関して
比較的ささいな問題がある.
この場合は交互作用を検定できる簡単な方法はない.
だからデーターは「つりあいがとれる」ようにとるしかない.
- すでに以前に議論しているように,
交互作用を検定してみて,
妥当であるなら交互作用項をプールするのは重要である.
これは12章で議論する.
- ひとつ以上の固定因子と
ひとつ以上のランダム因子からなる混合解析において,
検出力を計算するのは
またべつの面倒な問題である.
そもそも検定のためのF-分布だけど,
これを使って良い場合ってのは,
わずらわしい仮定の全てが満たされているときだけなのである.
- これらの仮定が破綻したときでも,
F-分布を使ってそんなに悪くないんじゃないかという
シミュレイションの結果も出ている.
いくつか仮定をゆるめてみても,
A に対するA
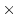 B の平方和の比はF-分布に従うらしい.
Box の検定というのがあって,
そういう状況でも使えるんだけど,
検出力は落ちるらしい.
B の平方和の比はF-分布に従うらしい.
Box の検定というのがあって,
そういう状況でも使えるんだけど,
検出力は落ちるらしい.
- とはいっても,
検出力を計算しようといういかなる試みにも
大きな問題がある.
さきほどの共分散の対称性がどーのこーのという制約が
満たされないかぎり,
統計量が従うべき確率分布が正確には計算できないのである.
その分布は「中央化されたF-分布」ではない.
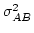 と
と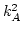 の間に相関があるからだ.
因子がランダムであっても
の間に相関があるからだ.
因子がランダムであっても
![[*]](foot_motif.png) 計算できないことには変わりない.
実験前にはF-分布に相当するものが計算できず,
とうぜん検出力も検定できない.
これまでの研究の歴史を振り返ってみると,
このような場合はシミュレイションを用いて検出力が計算されてきた.
計算できないことには変わりない.
実験前にはF-分布に相当するものが計算できず,
とうぜん検出力も検定できない.
これまでの研究の歴史を振り返ってみると,
このような場合はシミュレイションを用いて検出力が計算されてきた.
![[*]](foot_motif.png)
- 以上から,
混合モデルの使用にまつわる次の三つのことが示唆される.
まず,
これは生態学や生物学のその他の分野で使わなければならない,
ということである.
実験的操作をランダムに選んだ場所で行うのは
よくやる手口であるからだ.
- つぎに,
あらゆるものを反復せよ,
ということである.
- 最後に,
対立仮説を特定する固定因子の検定の検出力を計算したいなら,
二通りのやり方がある.
- 交互作用をプールできると仮定して,
「中央化されていないF-分布」を用いる.
これは8.3 節で説明しているものとまったく同じ.
- (交互作用をプールできるなら)
ランダム因子を検定するときに
(プールできないなら)
交互作用それ自身の検定のために
「中央化されたF-分布」を用いればよい.
- ある解析のなかで
二つの異なる処理がもたらす変異がどれくらいなのか
見積もりたい,
ということが結構あるものだ.
不幸にして,
これは生物学のいくつかの分野においては人気のある
やり口になってしまった.
Welden&Slauson (1986) が提案するところによれば,
変異(分散)全体の中である因子の変異が占めている比率が
その「重要性」に該当するというのである.
これは便利でもなければ比較可能な「測度」
![[*]](foot_motif.png) でもない
(Underwood&Petraitis, 1993 を見よ).
問題点は次の次の10.15.2 節で説明する.
でもない
(Underwood&Petraitis, 1993 を見よ).
問題点は次の次の10.15.2 節で説明する.
- ともかく最初にこの「測度」を提案した連中の話を聞いてみよう.
- ここでは例として,
何か動物の成長が「こみあい」(いつくかの密度水準を設定) と
「初期サイズ」(これもいくつかの水準を設定) によって決まると
考えている二因子の実験を考えよう.
- 密度の影響はTable10.13 のように見積もることができる.
こういうふうに計算したらいいんじゃないか
と提案されているんだが……:
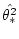 なんかの定義はTable10.13 を見てね.
なんかの定義はTable10.13 を見てね.
- しかし,まぁ,こういった測度を定義すると
いろいろと問題が出るのだ.
まず,
このような比較の問題として,
「おなじ基準ではかれない」(incommensurable) 成分
が含まれている.
これらはせいぜいのところ処理間の分散を比べる
「分散のような」測度として使えるぐらいだろう.
これらは分散ではない.
- つぎに,
これらの測度は相対値である.
たがいに独立な直交する因子の分散を解析するのが
この手法の利点なのに,
このやり方は比率を計算して互いに独立ではない
測度を作り出している.
- このような測度では,
たとえば,
二つのことなる場所で上の実験をやると,
「密度の重要性」といったことをこれら実験間で比較できなくなる.
- つまりこういう比較が意味をもつのは,
同じ実験の中だけであるようだ.
また測度はこのように:
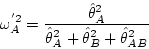 |
(30) |
定義したほうがまだしも論理的な正当化ができそうだ.
- ここにいたって,
いまなお,
克服しがたい問題が残されているのである.
あとで10.16節で議論する.
- すでに7.20 節で説明したように,
- 深刻なジレンマが
- 交互作用はこの問題の原因となるだろう
- シミュレイトつまりモデルによって
- 強度を推定するときの別の問題のひとつは
- しかしながら,
これは凄まじい汚染と対決しなければならないのである.
- 実験間や地域間で違いを推定しようという場合には
- だから,
異なる生息地や系で働いている過程を比較したいときには,
Experiments in ecology 輪読会メモ
This document was generated using the
LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 chp10e.tex
The translation was initiated by on 1999-12-09


1999-12-09
Back to Ex_Ecology index page
|
Back to Kubo's index page
![[*]](foot_motif.png)
![[*]](foot_motif.png) 一方で,
帰納的な仮説( a posterior)
一方で,
帰納的な仮説( a posterior)
![[*]](foot_motif.png) について調べている場合は,
以前に議論した
Type-I エラーに関する注意を思い出し,
Student-Newman-Keuls (SNK) 検定 あるいは
Ryan の検定
を行えばよい.
について調べている場合は,
以前に議論した
Type-I エラーに関する注意を思い出し,
Student-Newman-Keuls (SNK) 検定 あるいは
Ryan の検定
を行えばよい.![[*]](foot_motif.png) はこうなる:
はこうなる:
![[*]](foot_motif.png)
![[*]](foot_motif.png) )……
)……
![[*]](foot_motif.png) ある植物の数が,
ある場所では
日なたより日陰において極端に少なくなることもあれば,
べつの場所では
それほど数が変わらない場合があったとしよう.
これは食植者が日陰の葉を好み,
かつその虫がいる場所といない場所があるためにそうなっている
ものとする.
で,虫がつかないようにすれば,
日なたと日陰で植物の密度は変わらなくなるはずだ.
この仮説を調べてみよう.
ある植物の数が,
ある場所では
日なたより日陰において極端に少なくなることもあれば,
べつの場所では
それほど数が変わらない場合があったとしよう.
これは食植者が日陰の葉を好み,
かつその虫がいる場所といない場所があるためにそうなっている
ものとする.
で,虫がつかないようにすれば,
日なたと日陰で植物の密度は変わらなくなるはずだ.
この仮説を調べてみよう.![[*]](foot_motif.png) そんなものは設定しないことにしよう.
この実験には二つの直交する(orthogonal)
そんなものは設定しないことにしよう.
この実験には二つの直交する(orthogonal)
![[*]](foot_motif.png) 因子がある.
日なたか日陰か.
虫ありか虫なしか.
で,
仮説というのはこの二つの交互作用を予測しているのである
(つまり日陰かつ虫ありだと植物が減る).
因子がある.
日なたか日陰か.
虫ありか虫なしか.
で,
仮説というのはこの二つの交互作用を予測しているのである
(つまり日陰かつ虫ありだと植物が減る).![[*]](foot_motif.png) データー」に関して
比較的ささいな問題がある.
この場合は交互作用を検定できる簡単な方法はない.
だからデーターは「つりあいがとれる」ようにとるしかない.
データー」に関して
比較的ささいな問題がある.
この場合は交互作用を検定できる簡単な方法はない.
だからデーターは「つりあいがとれる」ようにとるしかない.![[*]](foot_motif.png) 計算できないことには変わりない.
実験前にはF-分布に相当するものが計算できず,
とうぜん検出力も検定できない.
これまでの研究の歴史を振り返ってみると,
このような場合はシミュレイションを用いて検出力が計算されてきた.
計算できないことには変わりない.
実験前にはF-分布に相当するものが計算できず,
とうぜん検出力も検定できない.
これまでの研究の歴史を振り返ってみると,
このような場合はシミュレイションを用いて検出力が計算されてきた.
![[*]](foot_motif.png)
![[*]](foot_motif.png) でもない
(Underwood&Petraitis, 1993 を見よ).
問題点は次の次の10.15.2 節で説明する.
でもない
(Underwood&Petraitis, 1993 を見よ).
問題点は次の次の10.15.2 節で説明する.
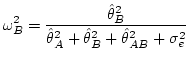
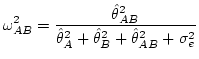
![[*]](foot_motif.png) REML のほうがML よりよい.
だいたい最尤推定量はモデルによっては収束しないじゃあないか.
REML のほうがML よりよい.
だいたい最尤推定量はモデルによっては収束しないじゃあないか.
![[*]](foot_motif.png)
![[*]](foot_motif.png) だからREML を使っても
別にいいことはなにもありませんからねっ.
だからREML を使っても
別にいいことはなにもありませんからねっ.
![[*]](foot_motif.png)
![[*]](foot_motif.png)