-
Metropolis-Hastings
(M-H) アルゴリズムを使った計算進捗状況はこんなかんぢで.
たとえば,
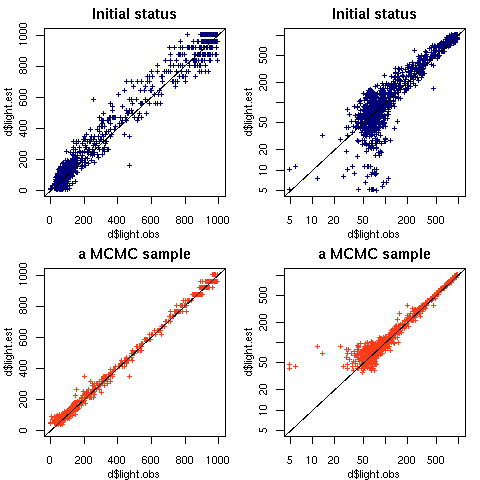
初期状態に対する最初の改良 step1 においては
葉っぱ消し去り (
Decrement)
を試み,
それによって対数尤度 (に比例する量)
が -31537 から -31521 に改善され
ACCEPT されて新しい状態として採択されている.
# Decrement: (-31537 vs -31521) ACCEPT 1: ll = -31521.7, nl = 7562
# Increment: (-31521 vs -31524) REJECT 2: ll = -31521.7, nl = 7562
# Increment: (-31521 vs -31595) REJECT 3: ll = -31521.7, nl = 7562
……(中略)……
# Increment: (-7706 vs -7741) REJECT 99994: ll = -7706.7, nl = 7092
# Increment: (-7706 vs -7706) ACCEPT 99995: ll = -7706.6, nl = 7093
# Decrement: (-7706 vs -7979) REJECT 99996: ll = -7706.6, nl = 7093
# Increment: (-7706 vs -7707) ACCEPT 99997: ll = -7707.2, nl = 7094
# Increment: (-7707 vs -7709) REJECT 99998: ll = -7707.2, nl = 7094
# Increment: (-7707 vs -7715) REJECT 99999: ll = -7707.2, nl = 7094
いっぽうステップ数が 10 万にちかいこのあたりでは,
対数尤度の変化はほとんどなくなり,
Gibbs 過程の定常状態といってもよい状態になっている
(このあたりでは尤度は単調に改善されず,
M-H 法ではある確率で「悪化」することも許容されている).
このような状態の林冠たちを sampling していく
(そして林冠の光合成生産のみつもりなどに使う).
定常状態における葉数は 7090 枚あたり,
となった
(初期状態では 7563 枚だった).
-
わかったことあれこれ.
-
葉っぱ増減のやりかた:
「こうしたら効率いいだろう」
と考えてたのはそれほど良くない,
とわかった
---
ランダムにハコを選んででたらめに葉っぱ出し入れやって,
M-H 法の ACCEPT/REJECT 裁定にまかせる,
といったしんぷるな手順が良いようだ
-
計算にすごく時間かかる
---
このように葉っぱ 7000-8000 枚ぐらいだと,
定常に到達するのに 10 万ステップぐらい必要?
-
初期状態やはり重要
---
言うところの「てきとーに決めた」初期状態は
(他のさらにでたらめな初期値に比べると)
格段に尤度が高く,
これのおかげで定常に到達するまでの時間は節約できてるよーな
気がする.
-
葉数などの (明示的な) 事前分布は必要か?
---
この問題ではポアソン分布などで
葉数の事前分布を仮定しないほうが良いのかもしれない
……
結果がこれにかなり左右されるんで
(ということで,
いま使ってるのは無情報事前分布)
-
収束判定は難しい
---
Full model や Null model の尤度を計算して,
deviance みたいなのも収束判定の参考にすべきかもしれない
いやー,
面白いけどたいへんですなぁ.
-
とりあえず一件落着したんで
1030 自宅発北大構内走.
曇天ときどきすこし雨.
1150 帰宅.
体重 72.2kg.
昼飯.
-
霜月さん
ところで少しらくがき.
R
で組みあわせ列挙するなら,
たとえば
library(gtools)
combinations(5, 3) # 5 個の中から 3 個とる組み合わせすべて
てなかんぢで
(CRAN の
gtools
が必要),
ケガれ言語 Perl のケガれ書法で同じこと書くなら
use Math::Combinatorics;
print join("\n", map { join(" ", @$_) } combine(3, (1 .. 5)));
としてみたり
(CPAN の
Math::Combinatorics
必要).
-
1300 自宅発.
雨.
1315 研究室着.
1325 研究室発.
ますますどしゃぶり状態.
北大クラーク会館地下の
理髪店
で散髪.
1430 終了.
2650 円.
雨あがっている.
研究室もどる.
-
研究室の共用マシン Dell 機
(Pentium4 2.4GHz)
で上の MCMC 計算やらせてみた.
私の ThinkPad X31 (PentiumM 1.6GHz) だと
55 分かかる 10 万ステップ計算が 22 分で終了した.
速い.
-
計算の顛末などをかくのごとくうだうだとぎょーむ日誌に書いてみたり.
-
お茶部屋で井田君と
モデル選択解説論文
(Johnson and Omland, 2004)
の話とか
……
だー,
また CANON のへっぽこ印刷機が
トナーぎれか.
ひとつの色がなくなっただけで印刷不能になるってのもなぁ.
-
母子里林冠 MCMC 計算について理解がススんだんで,
それにあわせて計算プログラム (in Perl)
りすとらしてみる.
よけーな変数や関数を削除していく.
-
母子里とは無関係の,
上の Combinatorics
(combination 列挙)
問題にちょっとはまりこんでしまう.
-
2030 研究室発.
小林さんと晩飯.
2140 帰宅.
-
Perl 自作関数による
combination 列挙問題の回答例つくって,
霜月さん
ところに投稿.
えー,
問題は N 個の中から k 個とるすべての組み合わせを列挙せよ,
というもの.
たとえば N = 5 で k = 3 だと
# 実行結果
1, 2, 3
1, 2, 4
1, 2, 5
1, 3, 4
1, 3, 5
1, 4, 5
2, 3, 4
2, 3, 5
2, 4, 5
3, 4, 5
と示せば良い.
-
解決策で一番簡単なのは,
上で述べたように R だろうが Perl だろうが
利他的なヒトたちのつくった library を利用すること.
しかしながら,
それがイヤだという場合はどうすればよいか.
Perl だとこういう
combo
なる関数を定義したらいいんじゃないの,
とゆーことで
……
#!/usr/bin/perl -w
use strict;
sub combo
{
my ($k, $array_orig) = @_;
my @array = @$array_orig; # copy
my @set;
if ($k == 1) {
@set = map { [$_] } @array;
}
else {
for (0 .. (scalar(@array) - $k)) {
my $head = shift @array;
push @set, map { [$head, @$_] }
@{&combo($k - 1, \@array)};
}
}
return \@set;
}
# 実行例 1
print join("\n", map { join(", ", @$_) } @{&combo(3, [1 .. 5])}), "\n\n";
# 実行例 2
print join("\n", map { join(", ", @$_) } @{&combo(3, ["a", "b", "c", "d"])}), "\n\n";
# 実行例 3
my $i = 1;
for my $s (@{&combo(4, [1 .. 8])}) {
print $i++, "\t", join(", ", @$s), "\n";
}
-
考えかたの基本は再帰で
(
&combo(3, [1 .. 4])
の場合)
-+-1-+-2-+-3
| | +-4
| +-3---4
+-2---3---4
とゆー「木」を作ればいいのである.
-
ぢつは似たような考えかたで解決する問題について,
すでに
去年 1/4
とか
去年 8/17
あたりですでに考えていたもんで.
-
[今日の運動]
-
[今日の食卓]
- 朝 (0810):
米麦 0.7 合.
コマツナあえもの.
卵焼.
- 昼 (1240):
うどん.
コマツナあえもの.
- 晩 (2100):