
φ
とすると光強度は cosφ
ってヤツですね
……
で,
葉数は高度の比例配分で加重,
と.
われながらいんちきくさい手法だな.
しかも,
この手ぬきでも
(とゆーか手ぬきではない光計算などそもそもありえん
わけだが)
葉っぱが「どっちを向いてるか」とか考慮せんといかんね.
これまた単位 vector の内積を計算すりゃいいんだな.
いやはや.


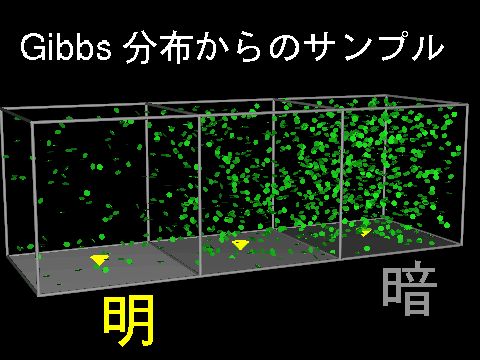
600cm × 300cm × 600cm
の空間が
60cm × 30cm × 60cm
のハコ 1000 個に分割されている
(後記: 高さは 720cm 必要).
そして,
おそらく葉っぱの三次元分布はランダムからはかけはなれた
集中分布になっているはずだ.
log(上の明るさ) - log(下の明るさ)
に比例する (直上からの光に関しては) というハナシの悪用である.
明るさの観測値が何か確率分布にしたがうと考えると
(このあたりいまいち理論的に弱いな)
log(上) - log(下)
の期待値が計算できるので,
これを重みとするというやりかただ.
観測には「上が暗くて下が明るい」
という場合も多々含まれているんだけど,
たたみこみ確率から計算する期待値は常に正なので,
どの box も葉っぱ存在確率がゼロにならない.