ぎょーむ日誌 2005-02-14

2005 年 02 月 14 日 (月)

• 0830 起床． 朝飯． コーヒー． 0920 自宅発． 雪． 0930 研究室着．
• R の survival pacakge を調査するプログラム作りあれこれ．
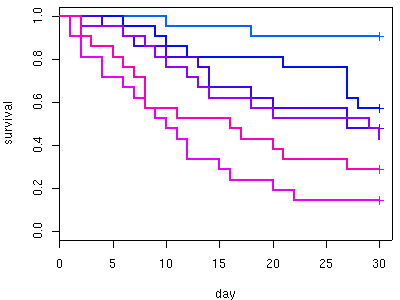
• 1140 どーにかこーにかできた． 下の図は plot.survfit で作図したもので 毒性によって生存曲線が異なる， という 架空のデータ (これは自作プログラム で生成したいわばシミュレイションの結果)． + は「うちきり」 (censored)， つまり実験期間 30 日間を生きのびたことをあらわす．

• この図のもとデータはこういうかんぢで．

  > Surv(data$time, data$status)
    [1] 30+ 30+ 30+ 30+ 30+ 30+ 30+ 30+ 18  30+ 30+ 30+ 30+ 30+ 30+ 30+ 30+ 30+
   [19] 30+ 10  30+ 30+ 30+ 30+ 30+ 27  21  30+ 30+ 30+ 30+  6   9  28  30+ 10 
   [37] 30+ 30+ 27  27  12  30+  4  18   7  27  30+ 20  30+ 30+ 30+ 30+ 14   6 
   [55] 30+ 10  30+ 30+ 27  14  13  30+ 30+ 30   8  30+ 13  20   2  30+ 30+  9 
   [73] 18  30+ 14  30+ 29   6  30+ 30+ 30+ 10  30+ 12   6  30+ 22  12   2  11 
   [91] 12  10  30+  7   9   4  16   1  20  30+  8   1   4  15   2  30+  2   3 
  [109]  2  27  16   8   5  30+  6  30+  8  21  30+ 30+ 20  17  30+  7  11   8 
  

  6 水準 × 7 ブロック × 3 個体． ここでも + は「うちきり」． ブロック間の差がそれなりにあり， 個体差もびみょーにある (どちらもガンマ乱数)．
• これを Cox の比例ハザードモデルへのあてはめ (関数 coxph() による) はこういうかんぢで． method = "exact" を指定してるけど， これは無視されて Breslow 近似になっとるような．

Call:
coxph(formula = Surv(time, status) ~ toxicity + frailty(plot), 
    data = data)
  n= 126 
              coef   se(coef) se2   Chisq DF p      
toxicity.L     2.090 0.478    0.478 19.13 1  1.2e-05
toxicity.Q    -0.874 0.452    0.452  3.74 1  5.3e-02
toxicity.C     0.177 0.374    0.374  0.22 1  6.4e-01
toxicity^4    -0.647 0.315    0.315  4.22 1  4.0e-02
toxicity^5    -0.214 0.297    0.297  0.52 1  4.7e-01
frailty(plot)                        0.00 0  9.3e-01
           exp(coef) exp(-coef) lower .95 upper .95
toxicity.L     8.083      0.124     3.168     20.62
toxicity.Q     0.417      2.396     0.172      1.01
toxicity.C     1.194      0.837     0.574      2.49
toxicity^4     0.524      1.910     0.282      0.97
toxicity^5     0.808      1.238     0.451      1.45
Iterations: 6 outer, 18 Newton-Raphson
     Variance of random effect= 5e-07   I-likelihood = -283.3 
Degrees of freedom for terms= 5 0 
Rsquare= 0.259   (max possible= 0.992 )
Likelihood ratio test= 37.7  on 5 df,   p=4.36e-07
Wald test            = 27.9  on 5 df,   p=3.83e-05

• この推定結果は， こちらがデータ生成プログラムで与えてたのと …… まあ， だいたい傾向としては正しいけど， 推定値はぜんぜん正確ではないように見える …… 例の選点直交多項式のおかげでわかりにくいものになっているが．
• しかし， ちょっとこれはズレが大きすぎるよーな …… なんかまた私がしくじってるんだろうか． いろいろと調べてみる．
• 上記 Cox 比例ハザードモデルはセミパラメトリックモデル である． じゃあ， パラメトリックモデル (指数関数的な減衰) を仮定した推定を survreg() 関数でやらせてみると ……

Call:
survreg(formula = Surv(time, status) ~ toxicity + frailty(plot), 
    data = data, dist = "exponential")
             Value Std. Error      z         p
(Intercept)  3.812      0.159 24.007 2.35e-127
toxicity.L  -2.068      0.476 -4.348  1.37e-05
toxicity.Q   0.880      0.451  1.949  5.14e-02
toxicity.C  -0.175      0.374 -0.469  6.39e-01
toxicity^4   0.637      0.314  2.028  4.25e-02
toxicity^5   0.207      0.297  0.698  4.85e-01
Scale fixed at 1 
Exponential distribution
Loglik(model)= -293.7   Loglik(intercept only)= -312.6
        Chisq= 37.81 on 5 degrees of freedom, p= 4.1e-07 
Number of Newton-Raphson Iterations:  6 23 
n= 126 

• うーむ …… どちらも推定法でも toxicity の影響がほぼ対数線形ってのは (これは乱数データ生成のときにそう設定したわけなんだが) ちゃんと推定できてるわけだが ……
• 昼飯． 窓の外は吹雪．
• 1300 から 1600 ごろまで生態科学専攻化の修論発表会． まあ， みなさん無事に終了， かな． 某研究隠匿師匠から知恵をさずけられて 「あれ? 液晶プロジェクターにつながらない」 と時間かせぎを試みたのがいたけど， けっきょくその 5 分間は発表時間に含まれなかったので ムダにおわった次第で．
• 研究室にもどると， 以前の査読の件であれこれと編集部から注文が …… いやはや， 私これ読まされるの三度めなんですが．
• とりあえず最小限必要な論点だけ作文して送信． 撤退． 1850 研究室発． 雪． 1900 帰宅． 運動． 晩飯．
• また R の生存解析 package 調査のつづき． 乱数生成シミュレイションにちょっとまずいところが見つかったので， 修正してみる． 上に示しているのは修正済のデータ・推定結果である． しかし， 推定結果があまり良いものに見えない， というところは変化ナシ． なんかまちがえてんのかなぁ．
• [今日の運動]
  • エアロバイク 50 分間． 右に続いて， 左ペダルのボールベアリングもイカれぎみ． 教訓: エアロバイクはペダルで選べ．
• [今日の食卓]
  • 朝 (0840): 米麦 0.7 合． ハクサイ・ブナシメジ・ワカメのシチュー．
  • 昼 (1230): 研究室お茶部屋． 米麦 0.7 合． ハクサイ・ブナシメジ・ワカメのシチュー．
  • 晩 (2210): 米麦 0.7 合． ホウレンソウ・ハクサイ・ブナシメジ・ワカメのシチュー．