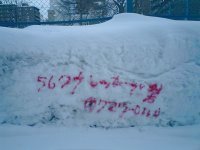
[雪壁上のらくがき]
これは無頼な若者の無軌道な表現活動の帰結ではなく,
北海道警察交通課の
「ここに路駐してた車はレッカー移動しました」
表示なのである.
うーむ.
Booth, J. G., Casella, G., Friedl, H. and Hobert, J. P. (2003). Negative binomial loglinear mixed models, Statistical Modelling, 3: 179-191.Poisson 分布をガンマ分布混合でばらつかせたのが 負の二項分布なんだけど, これにさらに正規乱数による random effects (個体差とかブロック差とか) を組み込んだもの. しかも Monte Carlo EM (MCEM) algorithm で計算します …… という何だかスゴいもので. 勉強になりそうだ.
glmmPQL()
では死亡率に関してブロック差の中に個体差がある,
という状況ではうまく推定できん」
と騒ぎまくっていた問題が解決した
……
これは
推定できなくて当然
だったのである.
嗚呼,
どうしてこんなあたりまえのことに気づくのに
えらく時間かかってしまったりするんだろう
(答: 統計学をよく理解してないから).
glmmPQL()
とかで「処理の差に加えて,
ランダム効果としてブロック差があってその中に個体差ある」
というモデルで生成した乱数データの
ブロック差・個体差をうまく推定できない理由は何だったのか,
を考えてみよう.
glmmPQL()
は錯乱した推定結果を出力していたのである.
これはブロック数を増やしたり,
あるいはブロック内の個体をいくら増やしても変わらない.
glmmPQL()
の視点にたってみると,
「個体差ぜんぜんナシ」
だろーが
「いや個体差とても大きい」
だろーが,
ともかく何であってもデータへのあてはまりかたはほとんど変わらない
(実際には乱数生成で作ったデータセットのちょっとした
偏りに左右されて「個体差ゼロ」⇔「個体差最大」
の間のどこかにさまよいこむ),
という状況なんで,
ああいう無茶苦茶な計算結果を出していたわけだ.
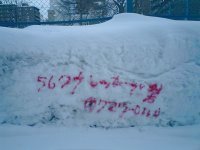
glmmPQL() 騒動」
の顛末を書く
……
なンか最近,
過去のぎょーむ日誌に
「後記」をつける機会が多いような気がする.
うかつな日々.