ぎょーむ日誌 2003-02-08

2003 年 02 月 08 日 (土)

• 1030 起床． うーむ， いいかげんに修論生周期はやめなくては． 朝飯． コーヒー．
• 破綻処理もそろそろイヤになってきたなぁ …… と怠業．
• 残念ながらいつまでも怠業できないので 1400 自宅発． 曇． 1415 研究室着．
• 低温研の加藤京子さんから Abies 伸びモデリングに関して いろいろとご教示いただく．
• 個体の高さ成長と階層構造の間に「交互作用」 とでもいうようなものがありうる……? かなり疑問に思いつつとりあえず推定してみようと思ったんだが …… 定式化のアイデアがうかばない． えーい， どちらも非負の値だということで， お試し推定方程式としてカケ算項を追加したものを でっちあげて計算してみると …… なンとかなり最大化尤度が向上してしまった．
• いやー， 推定式をよくよく検討しなおす必要あるんだけど， これは加藤さん言うところの
  「高さ成長の速い個体では樹冠下部は 横のび成長よくない」
  「高さ成長の遅い個体では樹冠下部の 横のび成長はそれほど悪くならない」
  …… ということなのかなあ．
• 面白そうだけど， 残念ながら現時点ではこれ以上モデルを複雑にするのは …… ちょっと避けたいところだ． ということで， 「その後」の懸案事項ということに．
• この計算やってるうちに， ある個体 i の 高さ成長項を log(Hi) だけでなく Hi でも計算させる 方法がわかった (初期値 scaling をケタにあわせて小さくするだけ ……ああ，なぜ気づかなかったのか)． おどろくべきことに， どちらでも最大化対数尤度はほぼ同じ (ずれは 0.01% ぐらい)．

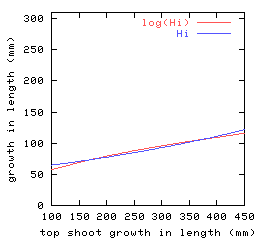
[高さ成長項はどうするか?] log(Hi) と Hi の推定結果 (期待値) の比較． このようにほぼ同じ． 式の意味としては exp 内の項は log(Hi) とするほうが伝統的なあろめとらーたちの 趣味に合致するんだろうけど (趣味うんぬんはたしかにそれなりに重要)， じゃあなんで言うところの 「ベキ乗式」 とやらでなくてはならんのか， というのがど素人の私なんぞにはわからないところで ……

• まあ， いろいろあって …… 夜中になぜか Fisher の正確確率検定 のプログラムを書いている自分を発見．
• じつはこの基本的な手法について自分はまったく理解していなかった， というのを発見してしまって． 言いわけするなら contingency table なんぞ作ったことなかったから． ともかく計算方法まるでわかっていなかった …… 3 時間ちかくもかけて， 2x2 行列専用の簡単な プログラム書いて結果を見て「あれヘンだな」 を繰り返しているうちに， よーやく何をやっているか理解できるようになってきた． じつに， いやはや．
• で調べたいパターンは 2x2 行列ではなく 2x3 になるかもしれないんで， しょうがないからその場合は R で計算 (最初からそっちをやれって?)．

	> budtable <- matrix(c(135, 314, 25, 74, 238, 7), nr = 3)
	> budtable
	     [,1] [,2]
	[1,]  135   74
	[2,]  314  238
	[3,]   25    7
	> fisher.test(budtable)

		Fisher's Exact Test for Count Data

	data:  budtable 
	p-value = 0.01467
	alternative hypothesis: two.sided 

• ゆーい差ありました …… と信じていいのかどうかよくわからないところで， 現在のサンプル数・事象発生確率のもとにおいて この検定方法って信用できんのか?
• ということで， せっかくつくった 2x2 専用 Perl プログラムで試してみる． まずは「ホントに同じモデルだった場合」 ということで
  • 無処理区 474 標本 (事象発生確率 p = 0.25)
  • 実験処理区 319 標本 (事象発生確率 p = 0.25)
  で危険率を 0.05 として， 10 回ランダムサンプルを与えてみると ……

	350 124 247 72	→ 0.275359
	356 118 243 76	→ 0.737150
	363 111 255 64	→ 0.294857
	352 122 235 84	→ 0.869039
	359 115 240 79	→ 0.932888
	329 145 244 75	→ 0.035344	ErrorI
	358 116 234 85	→ 0.506095
	365 109 238 81	→ 0.446209
	346 128 239 80	→ 0.565245
	350 124 233 86	→ 0.806051

おお， この標本数&確率だと 第一種の過誤ってのはほとんどおこらないわけね．
• じゃあ， 検定力のほうはどうなのか， と調べてみる． 「ホントに差がある (ホントにモデルが異なる) 場合」
  • 無処理区 474 標本 (事象発生確率 p = 0.28)
  • 実験処理区 319 標本 (事象発生確率 p = 0.23)
  ってのでランダムサンプル生成してみると ……

	350 124 242 77	→ 0.560353	ErrorII
	339 135 249 70	→ 0.046986
	328 146 248 71	→ 0.009275
	331 143 241 78	→ 0.089789	ErrorII
	338 136 239 80	→ 0.290445	ErrorII
	347 127 243 76	→ 0.362349	ErrorII
	345 129 246 73	→ 0.183942	ErrorII
	335 139 247 72	→ 0.040381
	329 145 249 70	→ 0.009051
	324 150 253 66	→ 0.000829

というかんぢで危険率を 0.05 とかにすると， けっこうな頻度で第二種の過誤が発生する． この設定では …… しかし contingency table の値がちょっとずれただけで table 発生確率って がたがたと変わるもんなのね．
• つまりこの標本数と事象生起確率の値， あ， それから「標本ごとに独立にある事象が確率 p で生起する」 と仮定する確率論的モデル (ベルヌーイ試行) のもとで 得られた contingency table に対して， Fisher の正確確率検定 (これはベルヌーイ試行とかは仮定してない) によって 「ゆーいでした」 という結果は「まあ大丈夫なのかなぁ」 なんだけど， 「帰無仮説棄却できませんでした」 となると 「ホントに差がないの?」 と疑うべきなのかもしれない …… とはいえ， これの逆の組み合わせよりはマシなんだろうな．
• AIC とかのモデル選択だとどういう結果になるのか? しかしもはやばて． そして生活周期のずれが悪化する方向に ……
• スケジューリング破綻の帰結として残り時間もない， ということは …… さんざん苦闘したあげくにこの問題も 「ゆーい差決戦主義」で終わるとは われながらホントに終わってるなと思いつつ (統計学的ゆーい差ではなく生態学的「有意差」を!) 2610 研究室発． まあ， 私にとってはナゾにみちた分割表の世界が少しだけわかった， というか実感できた， ということで． 2620 帰宅．
• [今日の運動]
  • 北大構内走 1600-1655． 肩こりその他を少しでも修復するために， ながくゆっくりと走る． ストレッチング．
• [今日の食卓]
  • 朝 (1130): パン． コーヒー．
  • 昼 : なんとなく食っていない． あ， 北大構内走のあとに少し食べた．
  • 晩 (2030): とくに匿名希望する料理人氏と院生たちが 準備してくれた修論なべ …… なぜか修論生はひとりもいなかったわけだが (にせ一名をのぞく)． タラ・豆腐のなべでうまかった．