|
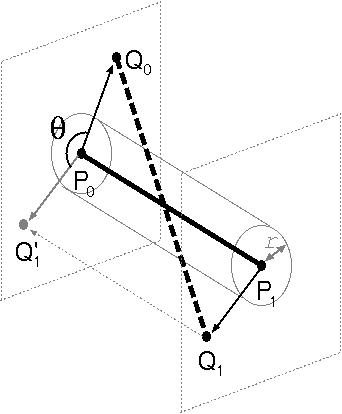
[円柱と直線]
点 {P0, P1}
をむすぶ線分を「中心軸」とする半径 r の円柱が
あるとする.
ある直線 L (太い点線) が
この円柱のどこかに「当たってる」を判断せよ
……
という問題.
中心軸と直行して 点 {P0, P1}
を含む平面と直線 L がぶつかる点を
点 {Q0, Q1}
とする (図参照).
|

|
[円柱と直線]
点 {P0, P1}
をむすぶ線分を「中心軸」とする半径 r の円柱が
あるとする.
ある直線 L (太い点線) が
この円柱のどこかに「当たってる」を判断せよ
……
という問題.
中心軸と直行して 点 {P0, P1}
を含む平面と直線 L がぶつかる点を
点 {Q0, Q1}
とする (図参照).
|
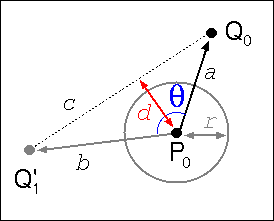
[P0 → Q0]
(長さ a) と
ヴェクトル [P1 → Q1]
(長さ b) を
点 {P0, Q0}
を含む平面
(どちらの平面を使ってもいいんだけど)
に投影してみる.
P0
の最小距離 d」を計算すれば
「当たり判定」ができる
(他にもいろいろと方法はあるんだけど).
この距離は d = (a b sin θ) / c
となる
(嗚呼,わりざん……).
|
A = [P0 → Q0]
とその長さの二乗 a2
を計算する.
B = [P1 → Q1]
とその長さの二乗 b2
を計算する.
γ = A・B
(各ヴェクトル各要素の積の和)
を計算する.
[P1 → Q'1]
の長さの二乗 c2
は余弦定理から
c2
= a2 + b2
- 2 a b cos θ
= a2 + b2 - 2 γ
となる.
d2
= (a b sin θ)2 / c2
= (1 - γ2)
/ (a2 + b2 - 2 γ)
を計算して
円柱半径の二乗 r2 と
大小を比較する.
mv kochi-mincho.ttf /usr/X11R6/lib/X11/fonts/TrueType

|