ぎょーむ日誌 2001-12-06

2001 年 12 月 06 日 (木)

• 0700 起床． 眠い．
• 朝飯・弁当の準備． 朝飯． コーヒー． シャワー．
• 0750 自宅発． 雨． 特急に乗って 0801 京急平和島発． 普通に乗り換えて 0830 京急上大岡発． 0845 研究所着．
• 昨日の「ぎょーむ日誌」に描出した ふつーの生態学者のふつーの生態に関して一読者より補足情報いただく．

  あえて付け加えるならば「どこで区分する」「どういう割り算を発 明する」「どんな線をひく」「どんな重回帰式を捻出する」……か が、「センス」と呼ばれる世界なのです。センス。

  …… おお，せんす． 同氏の指導教官はあまりにもこの種の「せんす」ばかりを強調するので， それに耐えかねた学生の中には 「ああ，自分には生態学の『せんす』がない!」 と絶望しつつ天を仰いだりする人もいるとか． まぁ， 我々はこんなせんすのいらない解析方法でものんびりと考えていきましょう．
• 「ニセ」アカマツを個体群的モデル化する推定問題に取り組んでるんだけど …… 最初の年のサイズ分布を何かパラメトリックな分布に 帰着させるのはまずい， ということに気づいた． と言うのも成長モデルを決めちゃってるので …… たとえば， 1 年目に対数正規分布をこじつけることができたとしても， 茎たちはみなさん勝手に成長してしまうから翌年には 必ず対数正規分布 (1 年目データから推定されたパラメトリックなる分布) からずれるんだよね．
• これの解決策として考えられるのは ……
  • 最初の年の推定サイズ分布として パラメトリックな分布を使わない．
  • サイズ分布は常に何らかのパラメトリック分布なのだ， という狂信にもとづいて， サイズ分布・成長サブモデル・死亡サブモデルを 全部同時に推定する．
  さーて， どっちがラクかな?
• いろいろと試行錯誤してるんだけど …… どちらも難しい． やはり「止まっているもの」を見てあたかもそれが「動いてる」 かのように思って計算するのは …… 心眼が必要ですなぁ． どうしたもんだろ．
• 気分転換に某秘密戦隊 (私は参謀かしらん?) の解析作戦に関するメイル． やはり「動き」の観測データがあるとモデリングは かなり容易だ． いくつか途中で見えていないところはあるけれど， そのへんは場合わけして和をとるとかで すらすらと尤度方程式を構築できる．
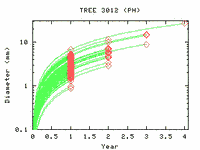
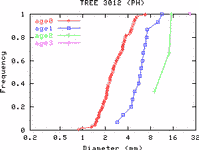
• 本業は進まぬまま午前終了． 昼飯． 弁当食ってるとアタマ内部の情報処理構造が変化したのか， 先ほどの 「茎たちはみなさん勝手に成長して …… ずれるんだよね」 問題を安直に片づける策を思いついた． これは死亡確率がサイズ (ここでは茎の基部直径としている) の関数として推定しようとするから難しくなるんだ． では， どうすればよいか? 「サイズの変化」(つまり成長速度) の関数とすればよいのである． いまのところ， 一番簡単に「齡に比例」とかしてるんで (下の図は 12/03 の「ぎょーむ日誌」から， 左の図のタテ軸と右の図のヨコ軸は対数目盛)．

これもまた詐術の一種なんだけど， (もともと使おうと思っていた) サイズ依存な死亡様式だって根拠ふりーだし …… やれやれ．
• さて， これは良いとして， 問題は関数型と推定方式． 上の図のデータを見てるうちにようやく気づいたんだけど， このままパラメーター推定すると， 値がすごくヘンなところに収束するな． たとえば成長速度 g の茎の死亡確率を exp(-m g) などと決めちゃうと， m の最尤推定値はかなーりでかくなる．
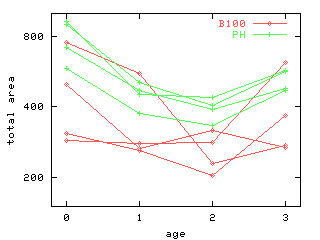
• またまた敵前大回頭． 「動き」は見えないけど 「動き」を制約する条件は決められるのではないか? このデータセットでは成り立っていないあの教科書的な架空概念 ―― パイプモデルだ． このいんちきくさい保存則もどきを組みこんで悪用すれば 御都合主義な計算結果が得られるような気がしてきた． 下の図 (11/26 の「ぎょーむ日誌」から) ながめると， 私の狙っているごまかしトリックに気づくかもしれない (邪拳ゆえに種明しはここまで)．

• どうすればいいだろうか． たとえば …… (新しく形成されつつある) 枝の先端ではぱいぴーじゃないんだけど， 根もとに近づくほど教条的になってくる， というような …… (これに似たアイデアはもともと 牧さん から教えていただいた，と記憶している)．
• …… もう 1645 か． いろいろ考えてみたんだけど， 未知パラメーター 1 個モデルで なんとかなりそうな気がしてきた． 問題はこの値をデータから推定できるかどうか， できるならどうしたらいいか． うーん， なんとかデータから値を一意に特定したいな． いろいろな場合について調べるのが面倒だから．
• う， 電話． 小川本校正がまだ続くのか …… で， ファクシミリみるとたしかにまだ間違いが残存． あのー …… どうして腐れ M$-Word なんぞで強制的に入稿させておいて， 数式にこんなに間違いがでるわけ? これって誰かが手で書き写してるわけじゃない． だったら LaTeX で入稿しても同じことぢゃん． いまさら文句言ってもしょうがないので， メイル返信で片づける．
• パラメーター推定のやりかたわからん． データからは推定できないもの， と仮定して現在の手続きの案を書いてみるか． 肥大成長は以前と同じとして， まずは子供茎の生成と分配．
  1. 親世代の茎を mother， その子供の茎を daughter とする．
  2. 子供の入る余地 Sm = a Σ mother.area を計算， a は個体ごとに推定された値．
  3. 条件 Sm > Σ daughter.area が成立するかぎりは， 子供プールから daughter をランダムに選び続ける．
  4. それぞれの mother において mother.vacant_area = a * mother.area， と設定．
  5. 子供は親を選ぶ． ある mother を選ぶ確率は f(mother, daughter) /Σ f(mother, daughter)， 関数 f(mother, daughter) = exp(-(mother.vacant_area - daughter.area)) ただし mother.vacant_area > daughter.area のとき (そうでない場合は確率ゼロ)．
  6. 子供に選ばれた親は mother.vacant_area -= daughter.area． ひとつもどって子供茎がすべてなくなるまで これを繰り返す．
  子供が親を選ぶなんで逆じゃん， と思うかもしれないけど， 親子関係のデータないんでこうするしかないのである． えーい， 問答無用 …… さて， 殺すほうはどうするか．
  1. 一番若い世代を除いて， すべての年齢コホートを 若い順に以下のように点検する．
  2. daughter をもたない mother は死亡．
  3. あるmother で daughter が死ぬ事象が生起する確率は 1 - exp(-r * g(mother)) で「パイプモデルからの逸脱」 g(mother) = (Σ daughter.area - mother.area)^2 が高いと子供が死にやすい． 時定数 r が推定できない (へぼい)． 小さい順に daughter を殺す (これもへぼい)．
  こんなところか．
• 値を特定できないパラメーター r については， シミュレイション結果を見て範囲を限定するしかないのか? 「20 年生のアカマツの非同化部の乾重は xx Kg ぐらいだから」 というふうに．
• プログラムはススまなかったけど， 少しだけ展望がひらけた． 1800 研究所発． 普通に乗って 1810 京急杉田発． 快特に乗り換えて 1820 京急上大岡発． 普通に乗り換えて 1840 京急川崎発． 1900 帰宅．
• いかん， 晩飯食ったら寝てしまった． いんちきでっちあげばて， か．
• 今日の食卓
  • 朝 (0710): 米 0.6 合． 昨晩の味噌汁の残り．
  • 昼 (1220): 弁当． 米 0.8 合． キャベツ・マイタケの炒めもの．
  • 晩 (1920): 米 0.6 合． 朝昼の残り．