ぎょーむ日誌 2001-12-03

2001 年 12 月 03 日 (月)

• 0700 起床． いつものごとく， 週末時差はあるけれど 土日にたくさん寝たので何とかなりそう状態． 今日は早寝すべきなんだろうか．
• 朝飯・弁当の準備． 朝飯． コーヒー． シャワー．
• 0740 自宅発． 晴れ． 特急に乗って 0750 京急平和島発． 普通に乗り換えて 0820 京急上大岡発． 0835 研究所着．
• どうも私は排気ガスを吸入しつつ歩いたり， 京急電車にゆられてるとアタマが働くようで …… 先週から考えてた「ニセ」アカマツの計算方法について 少しだけ発展した．

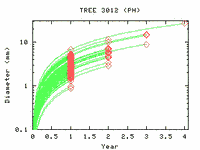
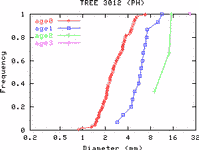
• 上のような二枚の図 (サイズの変化と年齢別のサイズ分布) を生成するようなモデルを考えていたわけだが …… 決められなかったのは， a → a+1 と年齢変化するときの茎 (あるいはシュート) の殺しかたであった． ちといんちきくさい定常性ごときものを仮定するのは仕方ないとして …… その上でどうすべきか? たぶん， このどちらかになると思う．
  1. サイズ分布を明示的に仮定しない → この場合は分布の下側を切って 分散が小さくなるようにする．
  2. 何かパラメトリックなサイズ分布 → この場合はサイズ依存な死亡率関数を データから特定する．
• このふたつだと， 1. のほうがラクではあるんだよね． 仮定の個数も (一見したところ) 少なくてすむし． ただしあまりにもごまかしが露骨なのだ． どうして植物を構成する部品がサイズ分布の記述統計量など 気にかけるだろうか? …… まぁ， そういうあたりで無理してるのがばれてしまう．
• では， 2. のほうはどうだろうか …… と考え直してみた． 齢 a における分布 f_{a}(x) と a+1 の f_{a+1}(x) をそれぞれ推定して， f_{a}(x) から f_{a+1}(x) に射影するような関数の推定を …… という方向に入り込んでしまっていた．
• これはスジが悪くて， むしろある齢におけるサイズ分布 f(x) が分かってるとしたときに， そのひとつ上の齢の集団のちらばりを見ながら サイズ依存死亡率 M(x | m) を推定する， としたほうがよいだろう． つまり f(x) だったものが

  f'(x | m) = f(x) (1 - M(x | m)) C(m)

  に変化する (m が推定すべきパラメーター)， というアイデアね． この C(m) は規格化のための量

  C(m) = 1 /∫(1 - M(y | m)) df(y)

  となる．
• しょうがないんで f(x) は何か簡単な確率分布として 齢 a のデータから求めておけば， あとは齢 a+1 のデータからパラメーター m を決めることができる． というのも， 尤度方程式が

  L(m) = Π f'(x_i | m)

  となって， あとはいつもどーりに推定できる (x_i が観測されたサイズ)．
• さて， そうすると f(x) はどういう分布だろうな． 対数正規分布， かな． しかしあまり奇麗にあてはまらないような ……
• お， 今朝も北大のサーヴァー hosho は不調か． ひょっとしてあれってカーネルのヴァージョンが ダメなやつだったかな? ともあれ， またまたかとー先生だのみな状況ですな． 先生は早起きなヒトでないので， しばらくこのままだろう．
• さて …… そもそもサイズを何にとるかだな． 昔の葉っぱは見えないので， また茎だけ考えるか (いやはや)． そうするとこいつは長さと基部直径が測定されてる． これらから導出される量としては体積， それから重量の憶測値．
• サイズは直径， とするか． 長さは最初の一年がすぎたら一定になってしまうし．
• 午前中はいろいろと関数型を検討していて終った．
• 昼飯の弁当食ってると甲山さんからメイル． かとー先生はまだ見えてない． なるほど． 昨晩， 院生部屋の階全体で短時間の停電． そうか二代目 hosho に無停電装置つけてなかったなぁ． おお， 浦口さんからもメイルが． ええ， 再起動がうまくいかないから電話しろ?? そんなこと言われたって， 音声によるリモートサポートは苦手なのに …… 時間稼ぎのメイルをやりとりしてると， よーやくかとー先生がオフィスに現れたそうである． 助かった． 1255 hosho 復旧． めでたしめでたし． 落ちたのは昨晩の 2250 ごろか．
• なんでも， 昨晩， 研究室内の極低温状態に生命の危機を感じた院生たちが， ついに耐えかねて部屋中の電熱線に 限界を超えた大電力を通電したために 札幌市北区一円が暗闇に閉ざされたとか (初代 hosho は無停電装置によってこの危機を回避した)． しばらく前から 北大建物内部はすでにプロパンガスも気化しない寒さで ガスストーヴは使えないし， 外聞ばかり気にする大学当局の指導によってダルマストーヴも 禁じられてしまったゆえのやむえぬ緊急非難だったのだ． 地球温暖化をいまや遅しと待望する 北日本の学舎ならではのできごとである．
• 午前中からくだんの推定方法を簡単な数式に帰着できないか 検討している．
  • f(x) = (対数正規分布)
  • M(x | m) = exp(-m x)
  ってのが簡単だと思うんだけど， f(x) の中で log(x) が出て来るから簡単ではないんだよね．
• じゃあ， f(x) が Weibull 分布ってのはどうだ …… これもちょっとややこしい． えーと， a x exp( -a x / 2) は Rayleigh 分布というのか． しかしこれはゼロから「立ち上がってる」 分布だしなぁ．
• うーむ， 今回も mlfitting で強引に解いてしまうか? もうちょっと安易な方法がないかどうかを調べてみよう．
• どうも簡単にはなりそうにないな． やはり数値的にやるしかないのかな? mlfitting を改造して対応すべきか． それとも R でプログラム組んでみるか? どっちにしても面倒だな ……
• R ノートみながら R を少しさわってみて， 今回はこれは使ったほうがよいのかどうか迷う． 尤度関数にわけのわからん定積分

  ∫(1 - M(y | m)) df(y)

  が入ってるんだけど， これは R の integrate() なる関数で数値的に計算できる． しかしながら， この関数の傾きも計算しないといけないんだよね． 数値微分は自分で定義するか?
• げ． JAMSTEC は腐れ firewall 交換のためだけに 三日間もネットを止めるのか．
• 計算問題 …… 推定すべきパラメーターは 1 個だけだから， この問題専用の最尤推定プログラム書くか? たとえばまたまた Perl とか? パラメーターがもひとつ増えたら終りだけどな． いやいや， CPAN に Math::MatrixReal なんてのもあるから逆行列計算だって簡単にできるぞ． 数値微分なんてのはてきとーに書いて …… ああ， もう何が何だかわからなくなってきた． 誰か助けてー
• よくわからぬままに Perl で推定プログラム書いてみることにする． なんか正気ではないねえ．
• 書きはじめて気づいたのだけど， この推定手法はちょっと変だ． 上で定常みたいな仮定がごにょごにょと書いてるあたりなんだけど …… よくないなぁ． 実験処理する前・後のサイズ分布を区別してない． 処理の影響うけてるのは最後の 1 年分だけだった． ああ， 対照区の個体たちに関しては， この推定のやりかたで問題ないのに．
• いったん撤退． 1755 研究所発． 普通に乗って 1810 京急杉田発． 特急に乗り換えて 1820 京急上大岡発． 1900 帰宅．
• 晩飯食ってから 「うー，計算プログラムとか問い合わせメイルとか書かなくては」 とでれでれ考えていたら， Linux の Emacs 上で動くメイラー Mew が不調になったため， この世界の全てに絶望しひどくすさみきったあげくに テロ予告まで口走るようになられた 某氏から Macintosh Eudra メイル． 某大某闇ネット内にごそごそともぐり込んで作業してると， 今度は北大からメイル． 修論生たちのすさみ対策として， お茶部屋に吉田戦車本を配架したとの浦口さんからのぎょーむ連絡． この時期における すさみケアの重要性をよく認識しておられる． やがてかわうそやつとむ君のように振る舞いはじめるであろう 修論生たちの姿を想像して しばし愉しむ．
• 結局， いつものごとく夜は仕事すすまず． よくわかってない点に関して 小林さんにお尋ねするメイルを書き． いまから 明日の飯の準備して寝る．
• 今日の食卓
  • 朝 (0715): 米 0.6 合． ハクサイ・タマネギ・シイタケの炒めもの．
  • 昼 (1220): 弁当． 米 0.8 合． 朝と同じ．
  • 晩 (1930): 米 0.6 合． ダイコン・ ハクサイ・タマネギ・シイタケの雑炊． ダイコン一本 30 円だったので帰り道 (旧東海道商店街) で買った． 一説によると青物市場があるので 大田区は野菜が安い， とか．