glm() で」
問題にとりくむ．
推定はうまくできてるようだけど，
「個体数」が多くないんで個体差がでない．
とゆーか，
個体差と処理の差が区別がつきにくい状況．
ともあれ，
これで一件落着．
tex2png.pl
の改良に
はまりこんでしまった．
glm()
系の関数でできてしまう，
という件について．
まず，
二項分布の尤度方程式を復習すると個体 i で
のうち
でなにかできごとが発生する．
そういう観測データあるときに，
発生確率
の二項分布モデルで説明しようとすると，
尤度方程式は
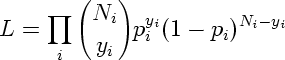
となる．発生確率
を
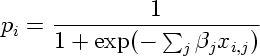
とすると， これはふつーの logistic 回帰ということになる． 尤度
を最大化する
たちを推定する，
ということで．
がつねに 1 であるとすると，
尤度方程式は
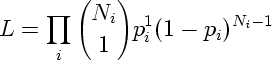
となる． これ見ればわかるように， 「あ，ほとんど幾何分布じゃん」 となるわけで ……
だった」
というデータがいろいろな個体についてあったとしよう．
このときに連続訪花数が幾何分布で表現できるとすると，
その尤度関数は
となる． ちがいは (推定すべきパラメーター)
を含まない
の部分だけで．
の最尤推定に関してはちょっとヘンな二項分布モデル
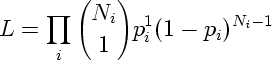
だろうがあるいは幾何分布モデルの
だろうが，
の最尤推定値はまったく同じになる．
この性質を悪用して，
glm() で幾何分布モデルの最尤推定をやってしまえばよい．
たとえば上の例を
R
で計算させたければ
glm(cbind(1, Ni - 1) ~ x, family = binomial(link = "logit"), ...)というふうにすればよい．
の部分は無関係であるからだ．
glmmML()
とか．
ただし glmmML()
の場合は上のような cbind()
わざが使えないので，
ちょっと工夫が必要になる
(今日の午前中もこの部分に苦闘してしまった)．
glm() うらわざ
「幾何分布だって logistic な推定だい」
でした．
- またしても三次元計算 (しかしプロトタイプは 「世の中なんでも一次元に決まってるんだ」 群落光合成モデル で代用する手口も可能)
- 三次元葉群配置をある種の Gibbs 点過程とみたてる Markov Chain Monte Carlo (MCMC) 計算
- 北大構内走 60 分間．
- 朝 (0800): 米麦 0.7 合． タマネギ・ニンジン・ピーマン・エリンギ・豚ハツのカレー．
- 昼 (1310): 研究室お茶部屋． 米麦 0.5 合． タマネギ・ニンジン・ピーマン・エリンギ・豚ハツのカレー．
- 晩 (2030): 米麦 0.9 合． タマネギ・ニンジン・ピーマン・エリンギ・豚ハツのカレー．