|
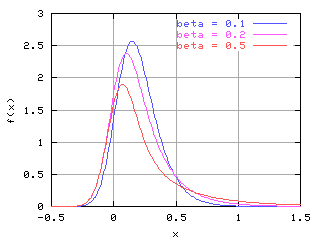
[Gamma + Gauss 分布]
Gamma 分布のばらつきを決める beta
と Gauss 分布のばらつきを決める sigma
を同時に決めないといけない
(左の図では sigma = 0.1).
もちろん Gamma の平均も.
Gauss 分布は人間の測定誤差をあらわすので
平均はゼロと仮定している
(ホントにゼロなんだろうか).
|
(観測された値) = (ある確率分布の標本) + (測定誤差)というような複数の確率分布の結合した状況 (というかスケイルパラメーターが複数ある状況) での推定問題にとりくむ. これは関数のたたみこみ, つまり数値積分を含むので, そのあたりをまず Perl コード化しないといけない.

|
[Gamma + Gauss 分布]
Gamma 分布のばらつきを決める beta
と Gauss 分布のばらつきを決める sigma
を同時に決めないといけない
(左の図では sigma = 0.1).
もちろん Gamma の平均も.
Gauss 分布は人間の測定誤差をあらわすので
平均はゼロと仮定している
(ホントにゼロなんだろうか).
|
|
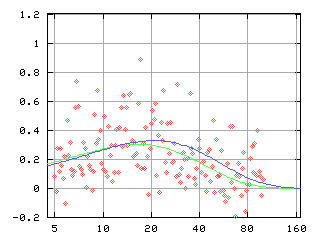
[それなりに良い推定結果の例]
青線が推定で緑線がホントの平均値. 標本数 152 コ. まぁ, よくがんばりましたとゆーことで. まだまだ検討・改良が必要ではあるけれど.
|